A candle is placed 14 cm in front of a concave mirror. The image of the candle is on a sheet of paper that is exactly 21 cm in front of the mirror. What is the magnification of the image? What is the focal length of this mirror?

1 Answer
Pallu
Sep 29, 2017

#M = -1 .5#
and
#f= 8 .4# cm

Explanation:

The radius of curvature #R# and the focal length #f# are to be taken as positive for a concave mirror.

Object distance #do = 14 cm #

Image distance #di = 21 cm#

As the image is on the same side of the object, #di# is to be taken positive.

Mirror formula :

#1/(di) + 1/(do) = 1/f#

#1/21 + 1/14 = 1/f#

# (2+3)/42 = 1/f#

# 5/42 =1/f#

#f = 42/5#

# f =8.4 # cm ---------focal length of the mirror.

Magnification formula in terms of object distance and image distance is given as:

#M = - (di)/(do)#

#M = - 21/14#

#M = - 3/2#

# M = - 1.5#
That means the image is real, inverted and enlarged.

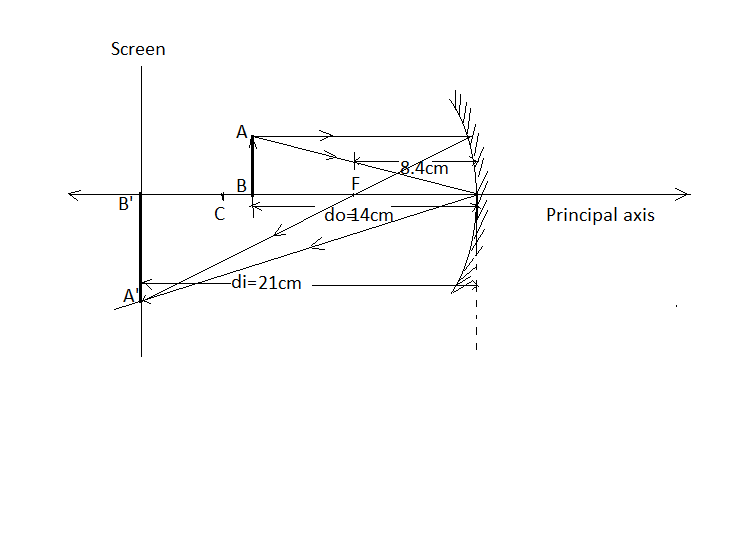
enter image source here

When the object is located between C and F, the image will be located beyond C.

In this case, the image is inverted (i.e., the right side up object results in an upside-down image).

The image dimensions are larger than the object dimensions as the absolute value of the magnification is greater than 1.

Finally, the image is a real image. Light rays actually converge at the image location. So the image of the object can be projected upon the sheet of paper.

Related questions
Impact of this question
19012 views around the world
You can reuse this answer
Creative Commons License