A charge of #-1 C# is at the origin. How much energy would be applied to or released from a # -3 C# charge if it is moved from # ( -1, -3 ) # to #(-2 ,7 ) #?
1 Answer
Explanation:
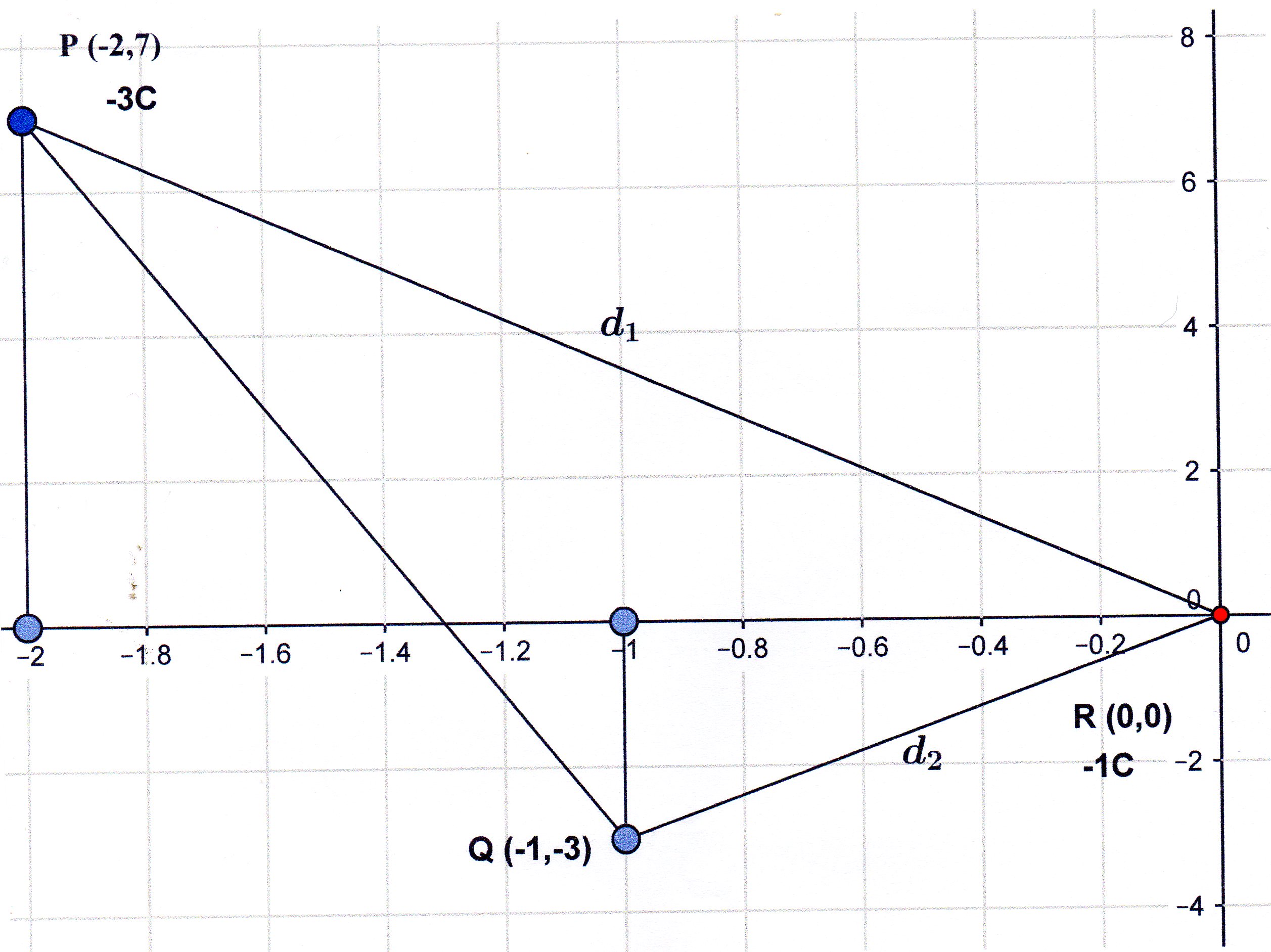
The -3C charge moves from
I will work out the electric potential due to the charge at the origin at points
Then I will subtract these to get the potential difference between the 2 points in volts
If 1C of charge is moved through a potential difference of 1 Volt then 1 Joule of work is done.
So I will then multiply the potential difference by -3C to get the total work done.
Potential at P:
This is given by:
To find
Potential at Q:
Again, we can use Pythagoras to find
To get the potential difference
To get the work done
The negative sign means work must be done on the charge to move it from
No units for distance are given. If it was in metres then

