A charge of #-2 C# is at #(4, 7)# and a charge of #-1 C# is at #( 1 , -6 )#. If both coordinates are in meters, what is the force between the charges?
1 Answer
Each charge experiences a repulsive force of
Explanation:
Let's start by creating a diagram of the information that we know:
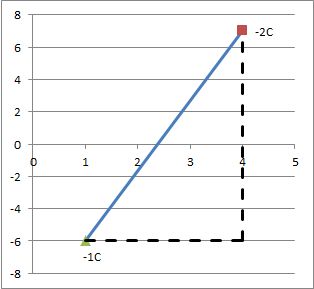
We know from Coulomb's Law that the force between charges depends on the size and sign of the charges, and on the distance between them:
Where
We can now get the force:
Each charge experiences this force which is repulsive, since they have the same sign of charge.
Advanced:
The constant

