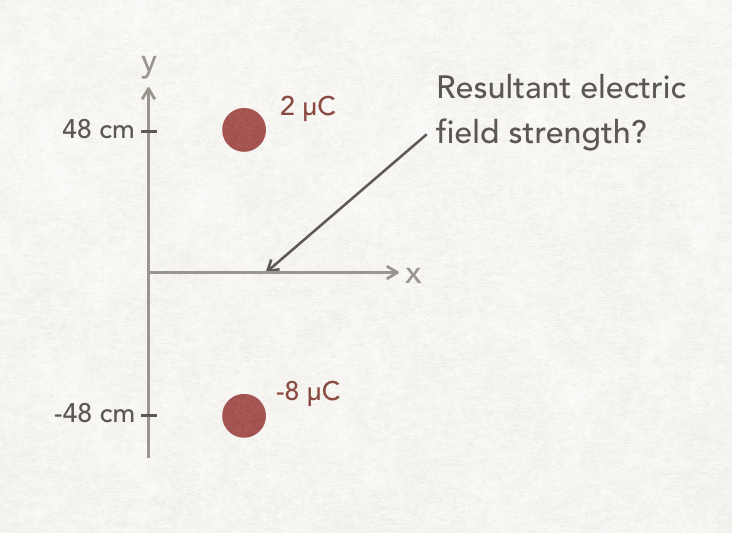
A charge of 2 μC is located 48 cm above the origin. A second charge of -8 μC is located 48 cm below the origin. What is the magnitude and direction of the net electric field at the origin?
1 Answer
Explanation:
First a diagram of the problem.
The equation relating electric field strength to charge and distance is:
There are two electric charges in the problem, each one creates an electric field in the space around it. We will calculate the strength of the field due to both of the charges and then sum them to find the resultant.
NB the charges have opposite signs (one is positive and one is negative) and they are on opposite sides of the origin, therefore the electric field vectors at the origin will have the same direction and they add up . The direction of an electric field vector is defined as being the direction a positive charge would move. A positive charge would be repelled by the 2 µC charge and attracted toward the -8 µC charge, i.e. the direction of the resultant field will be vertically downwards.
Calculate the individual field strengths:
NB because I have already addressed the directions of the fields above, in the calculations I only need to deal with magnitudes. I can therefore ignore the negative of the 8 µC charge.
Resultant electric field strength:

