A charge of #-3 C# is at #(-9,1 )# and a charge of #-1 C# is at #( 2,-5 )#. If both coordinates are in meters, what is the force between the charges?

Question

1246 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-12-27T17:25:37

#1.72xx10^(8)"N"#

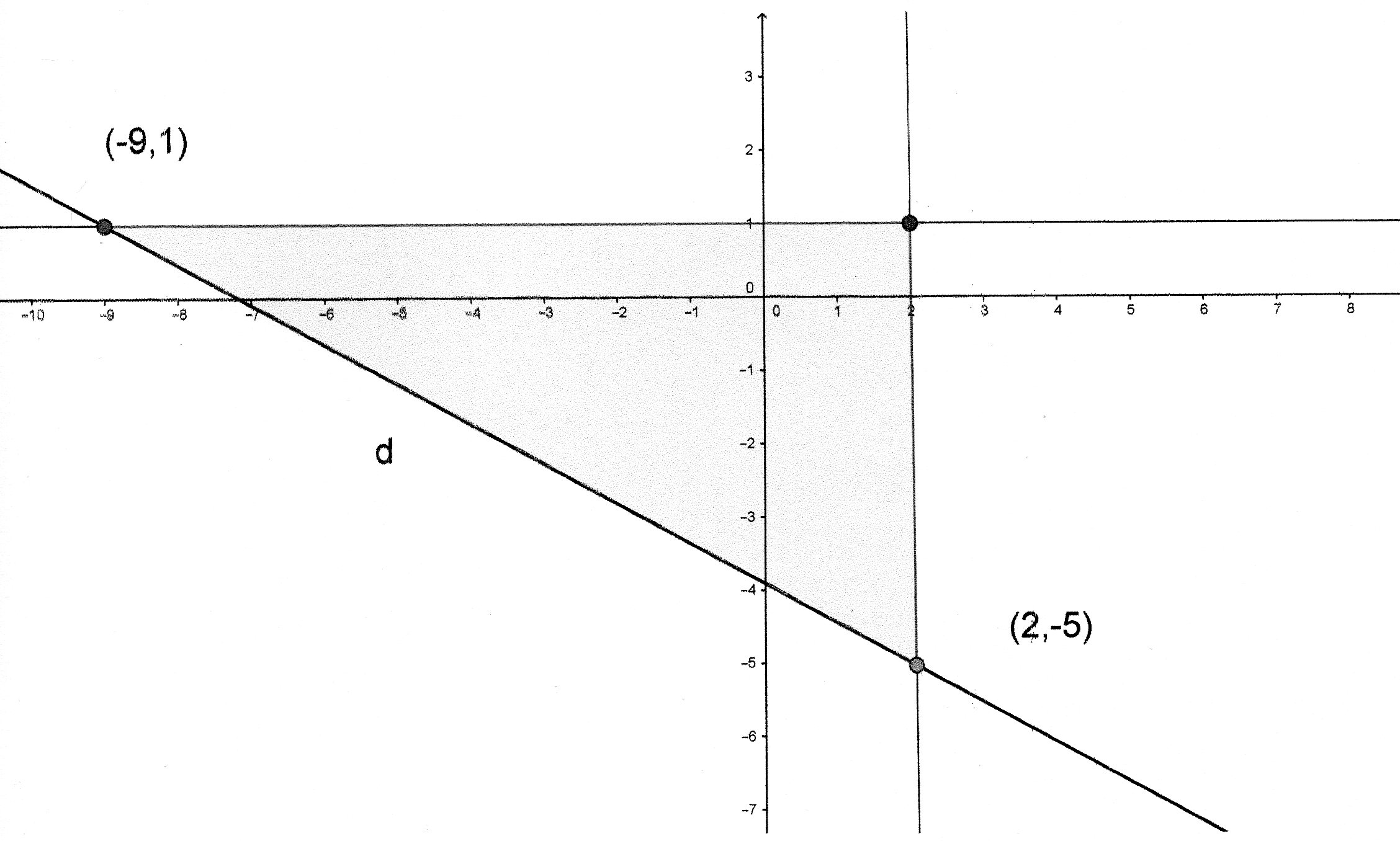
MFDocs

The distance #d# between the 2 points can be found by completing a triangle with #d# the hypotenuse.

The #x# displacement #=2-(-9)=11#

The #y# displacement #=1-(-5)=6#

So we can use Pythagoras to get #d# :

#d^2=11^2+6^2#

#:.d^2=157#

#d=12.53"m"#

#F=k.(q_1q_2)/d^2#

#k# is equal to #9xx10^9"F/m"# and is a constant :

#:.F=k.((-3)xx(-1))/12.53^2#

#F=(9xx10^9xx3)/157=1.72xx10^8"N"#