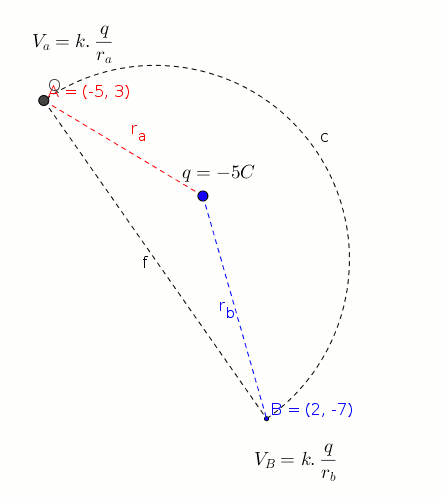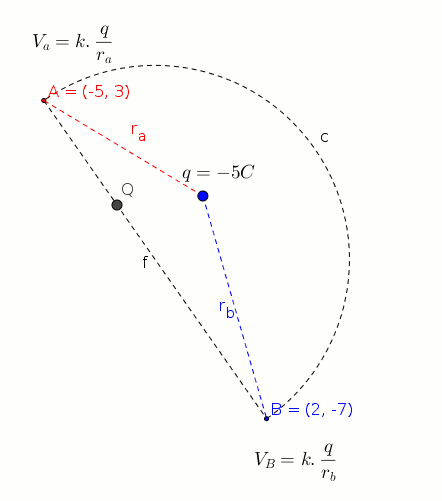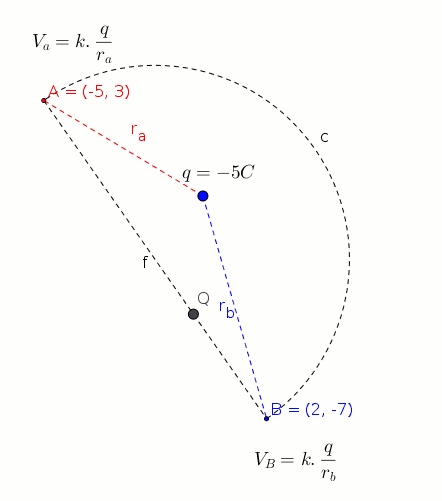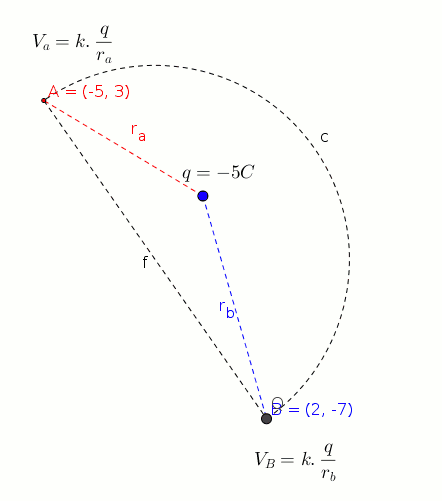
#"Since The electrical force is conservative,it is not important" #
#"that the charge have gone from A to B by which path.(f or c)."# #"Work doing both situation is the same."#
#"Since a charge of 4C moves in the electric field of the charge -5C,"#
#"we should find the potentials of the points A and B."#
#V_a=-k*5/(r_a)" , "V_b=-k5/(r_b)#
#r_a=sqrt((-5)^2+3^2)=sqrt(25+9)=sqrt(34)=5.83#
#r_b=sqrt(2^2+(-7)^2)=sqrt(4+49)=sqrt(53)=7.28#
#W=Q(V_b-V_a)#
#W=4(-k*5/r_b+k*5/r_a)#
#W=4*5k(1/r_a-1/r_b)#
#W=20k((r_b-r_a)/(r_a*r_b))#
#W=20k((7.28-5.83)/(7.28*5.83))#
#k=9*10^9#
#W=20k(0.034)#
#W=0.68*9*10^9#
#W=6.12*10^9" Joules"#

