Question

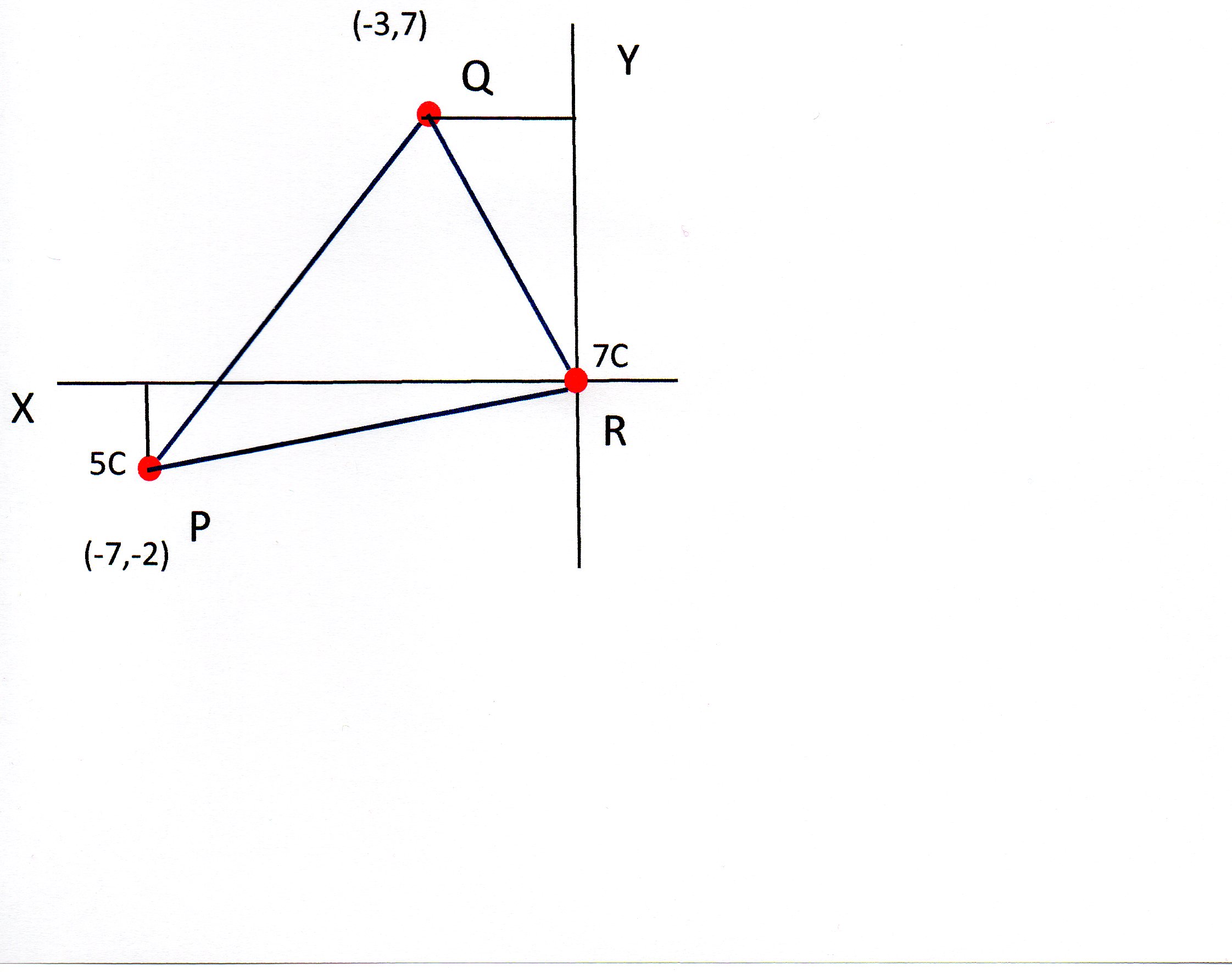
A charge of `7 C` is at the origin. How much energy would be applied to or released from a `5 C` charge if it is moved from `(-3 , 7 )` to `(-7 ,-2 )`?

Answer 1

`0.565"k"` units

Explanation:

MFDocs

I'll work out the electric potential at points P and Q.

Then I will use this to work out the potential difference between the 2 points.

This is the work done by moving a unit charge between the 2 points.

The work done in moving a 5C charge between P and Q can therefore be found by multiplying the potential difference by 5.

We need to find the length of PR and PQ which can be done using Pythagoras:

`PR^2=2^2+7^2`

`:.PR=sqrt(4+49)`

`PR=7.8`

and:

`QR^2=3^2+7^2`

`:.QR=sqrt(9+49)=6.93`

The electric potential due to a charge `q` at a distance `r` is given by:

`V=k.q/r`

`k` is a constant.

So the potential at point `P` is given by:

`V_P=kxx7/7.8=0.897k`

The potential at `Q` is given by:

`V_Q=kxx7/6.93=1.01k`

So the potential difference is given by:

`V_P-V_Q=k(0.897-1.01)=-0.113k`

So the work done in moving a 5C charge between these 2 points is given by:

`W=-0.113kxx5=-0.565k"units"`

This is the work done on the charge.

There are no units of distance given. If this was in meters then `k=9xx10^9"m/F"` and the answer would be in Joules.