A chord with a length of #12 # runs from #pi/12 # to #pi/8 # radians on a circle. What is the area of the circle?

Question

1411 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-07-28T15:01:23

The area of the circle is #=26439.6u^2#

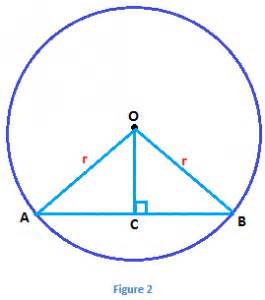
enter image source here

The angle subtended at the centre of the circle is

#hat(AOB)=theta=pi/8-pi/12=3/24pi-2/24pi=1/24pi#

The length of the chord is

#AB=12#

#AC=12/2=6#

#sin(theta/2)=(AC)/r#

The radius of the circle is

#r=(AC)/sin(theta/2)=6/sin(1/2*1/24pi)=6/sin(1/48pi)=91.7u#

The area of the circle is

#area=pir^2=pi*91.7^2=26439.6u^2#