Question

A chord with a length of `6` runs from `pi/12` to `pi/2` radians on a circle. What is the area of the circle?

Answer 1

Area of the circle is `30.3` sq.unit.

Explanation:

Formula for the length of a chord is `L_c= 2r sin (theta/2)`

where `r` is the radius of the circle and `theta` is the angle

subtended at the center by the chord.

`theta= pi/2-pi/12 = 90-15=75^0`

`:. L_c= 2 * r * sin (theta/2) ; L_c=6 , theta=75^0` unit or

`r= 6/(2 * sin 37.5) =3/sin 37.5~~4.93` unit.

Area of the circle is `A_c=pi*r^2= pi*4.93^2~~76.30(2dp)`

sq.unit [Ans]

Answer 2

Area of circle `A_c ~~ color(purple)(76.2942)`

Explanation:

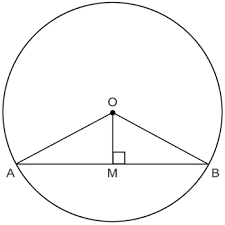
Chord length `AB =Ch = 2 * r * sin (theta/2)` where `theta` is `/_(AOM)`

`theta = /_(AOM) = theta = (pi/2) - (pi/12) = (5pi)/12`

`theta / 2 = ((5pi)/12) / 2 = (5pi)/24`

Given Chord length `AB = Ch = 6`

`r = 6 / (2 * sin ((5pi)/24) ~~color(blue)(4.928)`

Area of the circle `A_c = pi r^2 = pi * (4.928)^2`

Area of circle `A_c ~~ color(purple)(76.2942)`