A circle has the radius of 15 inches. What is the length of the arc intercepted by a central angle of 120 degrees?

Question

12605 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-02T05:23:16

#" "#
#"Length of the Arc"# #color(blue)(~~ 31.42 " inches"#

#" "#
#color(green)("Step 1":#

Construct a circle using the given Radius (r) = 15 inches.

With a Central Angle of #color(red)(120^@#, using two radii, a sector is created:

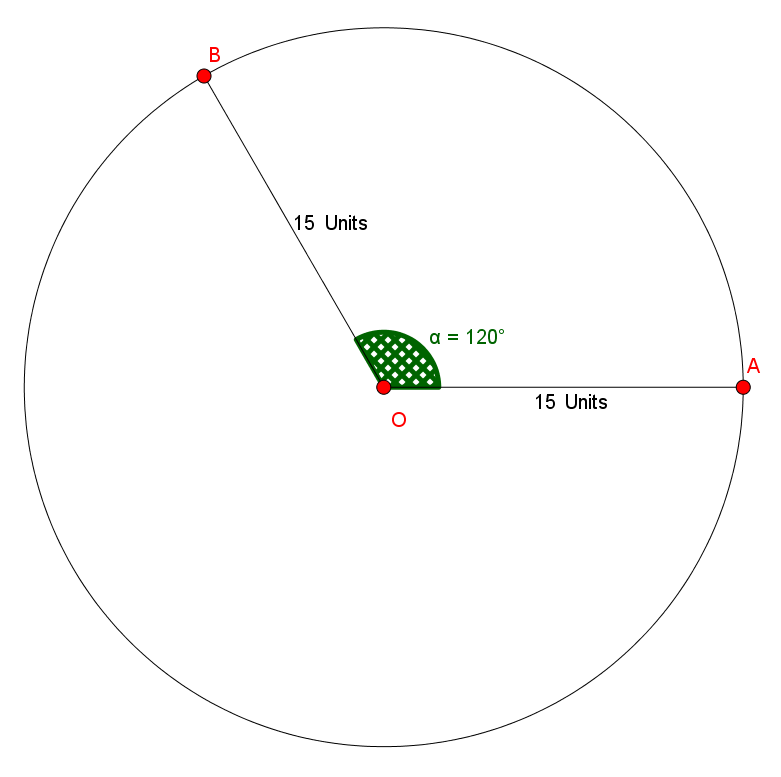
enter image source here

#color(blue)(Radii: OB = OA = "15 inches"#

#color(blue)("Central Angle: "/_AOB = alpha = 120^@#

#color(green)("Step 2":#

Find the Circumference (C):

Formula: Circumference (C): #color(red)(2* pi* r)# Units.

#color(red)(pi# is the ratio of the circumference of a circle to its diameter.

For many purposes you can use #color(green)(3.14159#

#rArr C = 2*pi*15#

Using a calculator:

#C~~94.24777961#

#color(green)("Step 3":#

To find the Arc Length use the formula: #color(brown)(theta^@/360^@*Circumference)#

#rArr theta^@/360^@*Circumference#

#rArr (120^@/360^@)*94.24777961#

#rArr (1/3)*94.24777961#

Using a calculator:

#rArr ~~ 31.41592654#

Hence,

Arc Length: #~~ 31.42# inches.

#color(green)("Step 4":#

Verify the final result using a construction in Geometry:

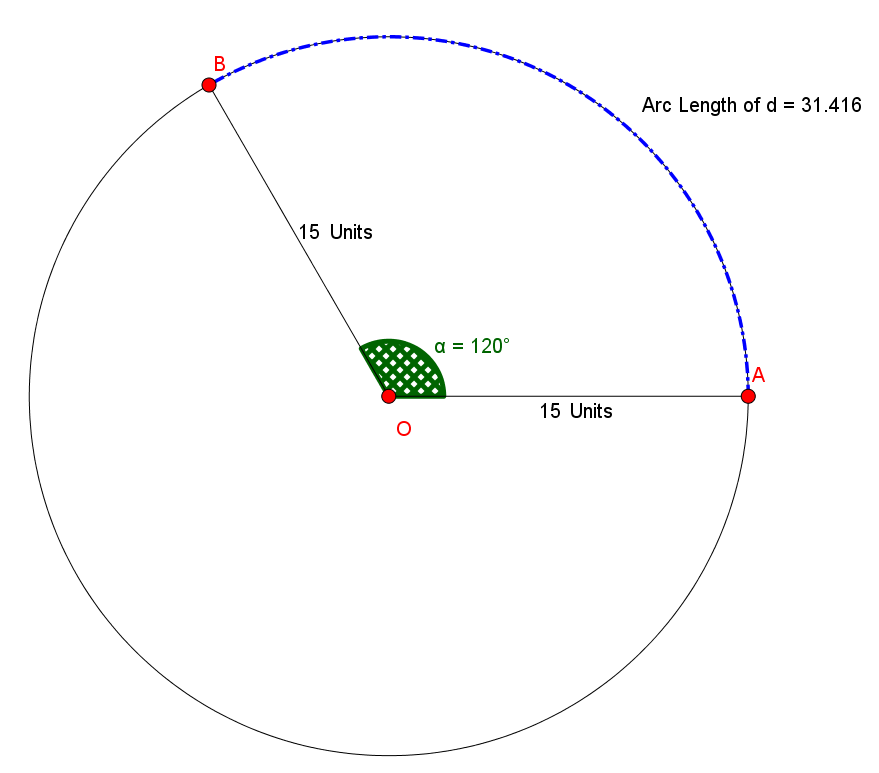
enter image source here

Hope it helps.