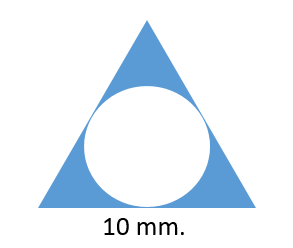
A circle is inscribed in an equilateral triangle with a side length measuring 10 mm. Represent the area of the shaded region as a percentage of the total area of the triangle?
1 Answer
Mar 28, 2018
see explanation
Explanation:
Area of an equilateral triangle
given side length
Let
formula for inradius of the incircle of the triangle :
shaded area
ratio of
