A circle touches two perpendicular lines #2x-3y=15# and #3x+2y=3# at the points #A(6,-1)#, #B(1,0)# respectively. Find the equation of the circle?
2 Answers
Explanation:
The tangent to a circle
at the point
Thus, the tangent at
or
Since this is the line
Again, the tangent at
or
Since this is the line
Hence
Thus
So,
and
Thus the circle is
Explanation:
The following is a graph of:
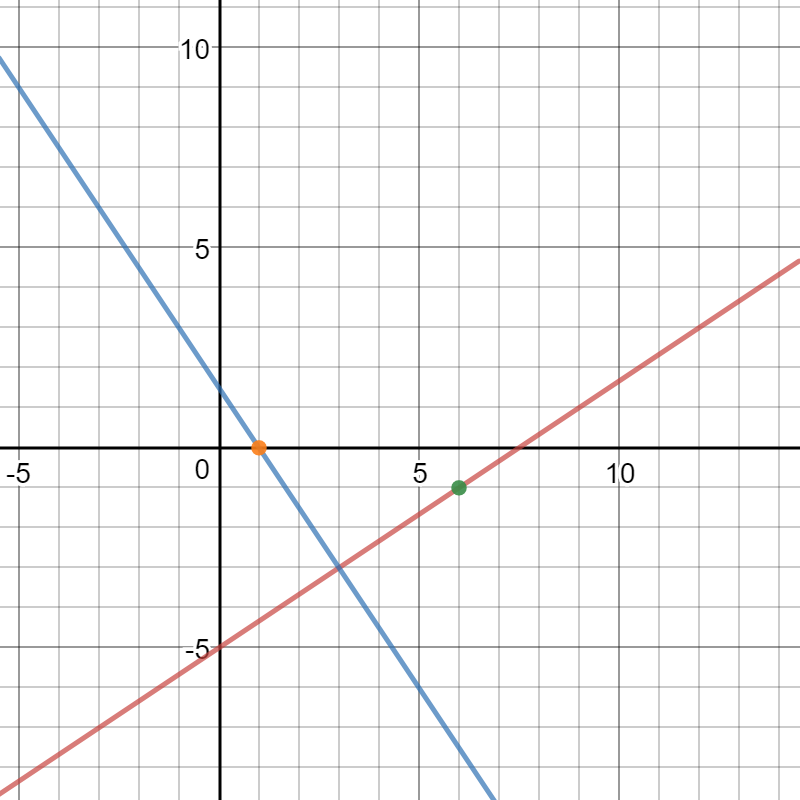
Because the center must be located on lines that are perpendicular to the points of tangency, we can use equations [1] and [2] to write two equations that must intersect at the center.
Set equation [1] equal to an arbitrary constant,
Set equation [2] equal to an arbitrary constant
Substitute point B into equation [1.1] and solve for
Substitute the above into equation [1.1]:
Substitute point A into equation [2.1] and solve for
Substitute the above into equation [2.1]:
Add equations [1.2] and [2.2] to the graph:
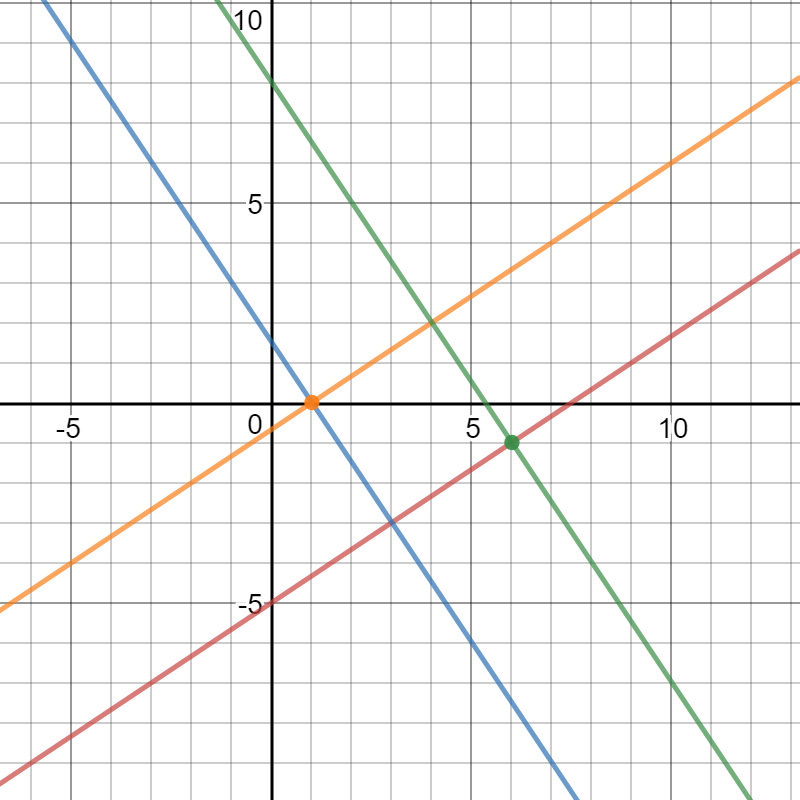
Please understand that the center of the circle must be at the intersection of equations [1.2] and [2.2], therefore, we shall solve them as a system of equations:
The center of the circle is at the point
The standard Cartesian equation of a circle is:
where
Substitute point C into equation [3]:
To find the radius, we shall substitute point B into equation [3.1]:
Substitute the above into equation [3.1]:
Add equation [3.2] to the graph:
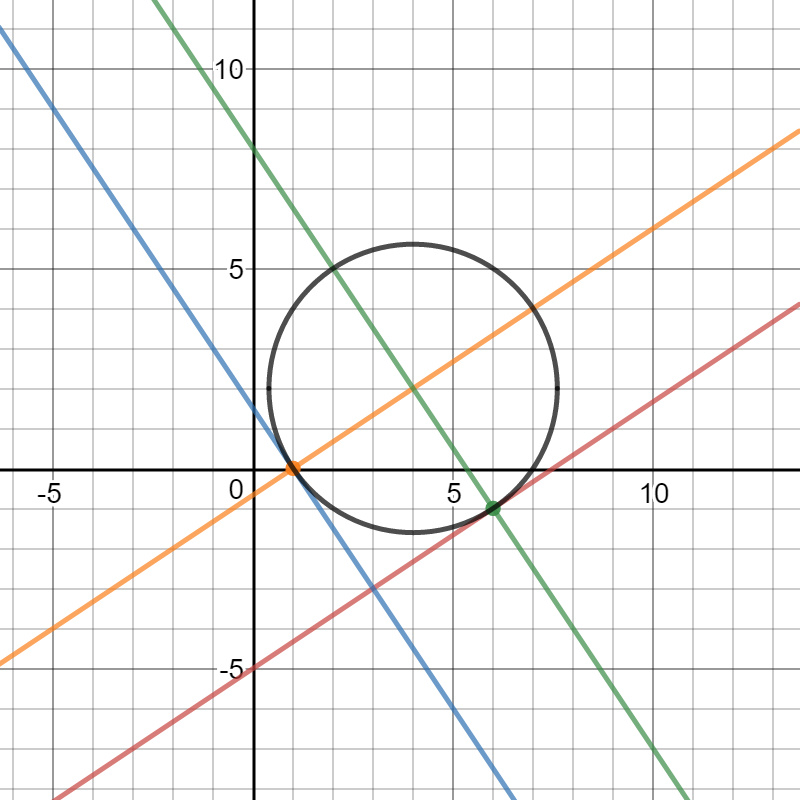
Please observe that equation [3.2] touches [1] and [2] and points A and B respectively, therefore, equation [3.2] is the correct equation of the circle.

