A cone has a height of #12 cm# and its base has a radius of #2 cm#. If the cone is horizontally cut into two segments #6 cm# from the base, what would the surface area of the bottom segment be?

Question

1338 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-21T11:12:49

#:.color(purple)(=69.9cm^2# to the nearest 1 decimal place #

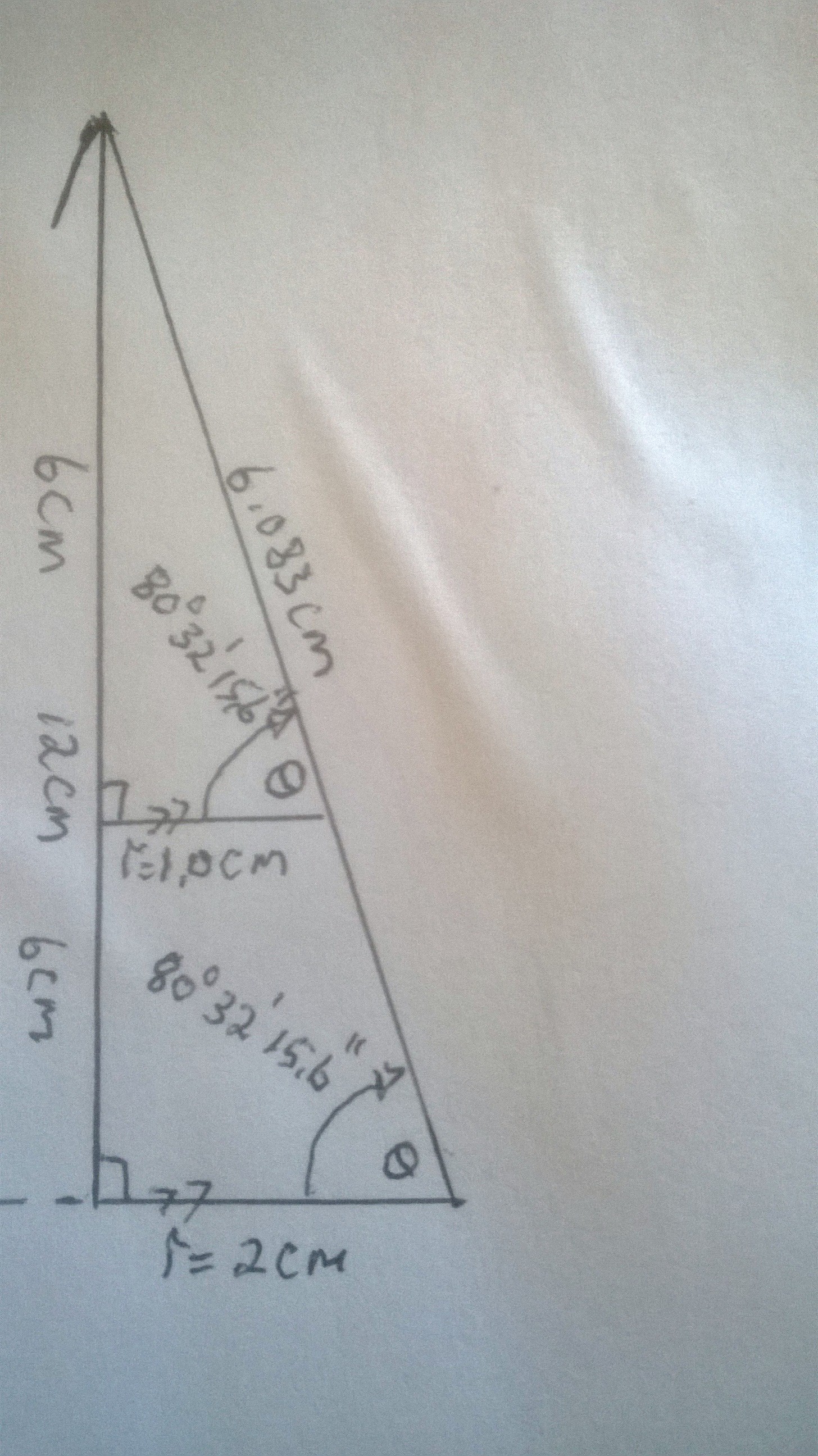
enter image source here

:.Pythagoras: #c^2=12^2+2^2#

#:.c=L=sqrt(12^2+2^2)#

#:. c=Lcolor(purple)(=12.166cm#

#:.12/2=tan theta=6=80^@32’15.6”#

:.#color(purple)(S.A.#= pir^2+pir*L#

:.S.A.#=3.141592654*2^2+pi*2*12.166#

:.S.A.#=12.566+76.441#

:.Total S.A.#color(purple)(=89.007cm^2#

#:.Cot 80^@32’15.6”*6=1.0cm=#radius of top part

:.Pythagoras: #c^2=6^2+1.0^2#

#:.c=L=sqrt(6^2+1.0^2)#

#:. c=Lcolor(purple)(=6.083cm# top part

:.S.A. top part#=pi*r^2+pi*r*L#

S.A. top part#:.3.141592654*1.0^2+pi*1.0*6.083#

S.A. top part#:.=3.141592654+19.110#

S.A. top part#:.color(purple)(=22.252cm^2#

:.S.A. Botom part#color(purple)(=89.007-22.252=66.755cm^2#

The total surface area of the bottom part got to include
the surface area of the circle of the top part.

:.S.A. Botom part:.=3.142+66.755=69.897 cm^2#

#:.color(purple)(=69.9cm^2# to the nearest 1 decimal place #