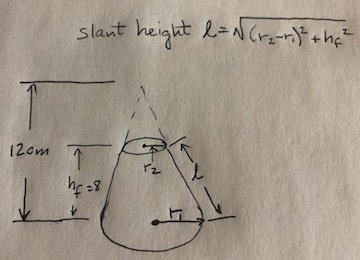
Given: cone of #h= 12 cm, b = 8 cm#. Cut #8cm# from the base. Find the surface area of the bottom segment.
The new shape is called a conical frustum . It has the surface area formula :
#A = A_"lateral" + A_"bases"#
#A_"lateral" = pi (r_1 + r_2) sqrt((r_1 - r_2)^2 + h_f^2)#
#A_"bases" = pi((r_1)^2 + (r_2)^2)#, where
#r_1 = "base radius = 8 cm", " "r_2 = "top radius" = ?,#
#h_f = "the height of the frustum" = 8 cm#
#h_"top cone"/h_"bottom come" = (12-8)/12 = 4/12#
#color(blue) "Find the radius of the top"# using proportions of the two cones:
#h_"top cone"/h_"bottom come" = r_2/r_1; " "4/12 = r_2/8#
Use the cross-product: #12 r_2 = 4*8 = 32#
#r_2 = 32/12 = 8/3 cm#
#A_"lateral" = pi(8 + 8/3) sqrt((8-8/3)^2 + 8^2)= 32/3 pi sqrt((16/3)^2 + 64)#
#A_"lateral" = 32/3 pi sqrt(256/9 + 576/9) = 32/3 pi sqrt(832)/3#
#A_"lateral" = 32/9 pi sqrt(16) sqrt(4)sqrt(13) = 32/9 pi *8 sqrt(13)#
#A_"lateral" = 256/9 sqrt(13) pi " "cm^2#
#A_"bases" = pi(8^2 + (8/3)^2) = 640/9 pi " "cm^2#
#A = (640/9 + 256/9 sqrt(13)) pi ~~ 173.7 pi " "cm^2 ~~549.6 " "cm^2#