A crane lowers a 600kg generator by attaching 4 cables to it at an angle of 67° compared to the horizontal. The generator moves at a rate of -2.12m/s². How much tension is on each cable?

1 Answer
A08
Feb 29, 2016

#=1253.12N# rounded to 2 places of decimal

Explanation:

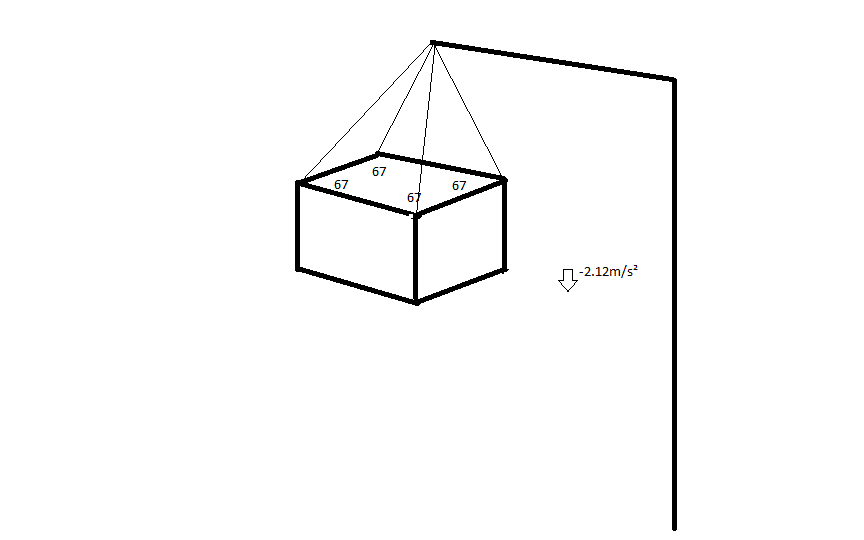
mycomputer

See figure above.

Let #T# be the tension in each cable. Assuming all cables to be similar. Each cable is making an angle of #67^@# with the horizontal.

The vertical upward component of tension in each cable#=Tsin 67^@#
#=0.92050T#
Total vertical upward component of tension in all 4 cables#=4xx0.92050T#
#=3.6820T#

The generator is being acted upon by two forces.
1. Weight given by #g=9.81ms^-2#
2. Downward acceleration #=-2.12ms^-2#

As the downward acceleration is in the direction of gravity hence net downward force is given by#=9.81-2.12=7.69ms^-2#

Net downward force #=mxxa=600xx7.69=4614N#

Equating the total vertical tension with net downward force we obtain
#3.6820T=4614#
or #T=1253.12N# rounded to 2 places of decimal

Related questions
Impact of this question
991 views around the world
You can reuse this answer
Creative Commons License