Question

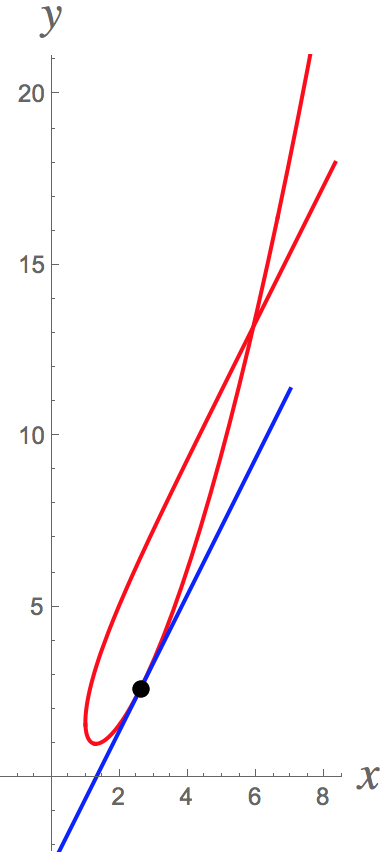
A curve has parametric equations x= 2t-ln 2t and y= t² - ln t² where t>0 . Find the value of t at the point on the curve where dy/dx=2 . Hence find the coordinates of that point?

Answer 1

`dy/dx=2` when `t=2`. The coordinates of the corresponding point are `(x,y)=(x(2),y(2))=(4-ln(4),4-ln(4)) approx (2.61,2.61)`.

Explanation:

We have `dx/dt=2-1/t=(2t-1)/t` and `dy/dt=2t-2/t=(2t^2-2)/t`. Therefore `dy/dx=(dy/dt)/(dx/dt)=(2t^2-2)/(2t-1)=(2(t^2-1))/(2t-1)`.

Setting `dy/dx=2` results in `(t^2-1)/(2t-1)=1`, or `t^2-1=2t-1`, or `t^2-2t=t(t-2)=0`. The solutions of this equation are `t=0, 2`. However, `t=0` is not part of the domain (`t>0`) of the original parametric curve.

Therefore, `dy/dx=2` when `t=2`.

Since `x(2)=4-ln(2)` and `y(2)=4-ln(2)`, the coordinates of the corresponding point are `(x,y)=(x(2),y(2))=(4-ln(4),4-ln(4)) approx (2.61,2.61)`.

Here's a picture of this situation: