A cylindrical industrial storage tank has a surface area-to-volume ratio of 3. If the height of the cylindrical tank is 2 meters, what is the radius?

Question

3812 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-05T20:33:15

I got #r=1m#

I tried this:
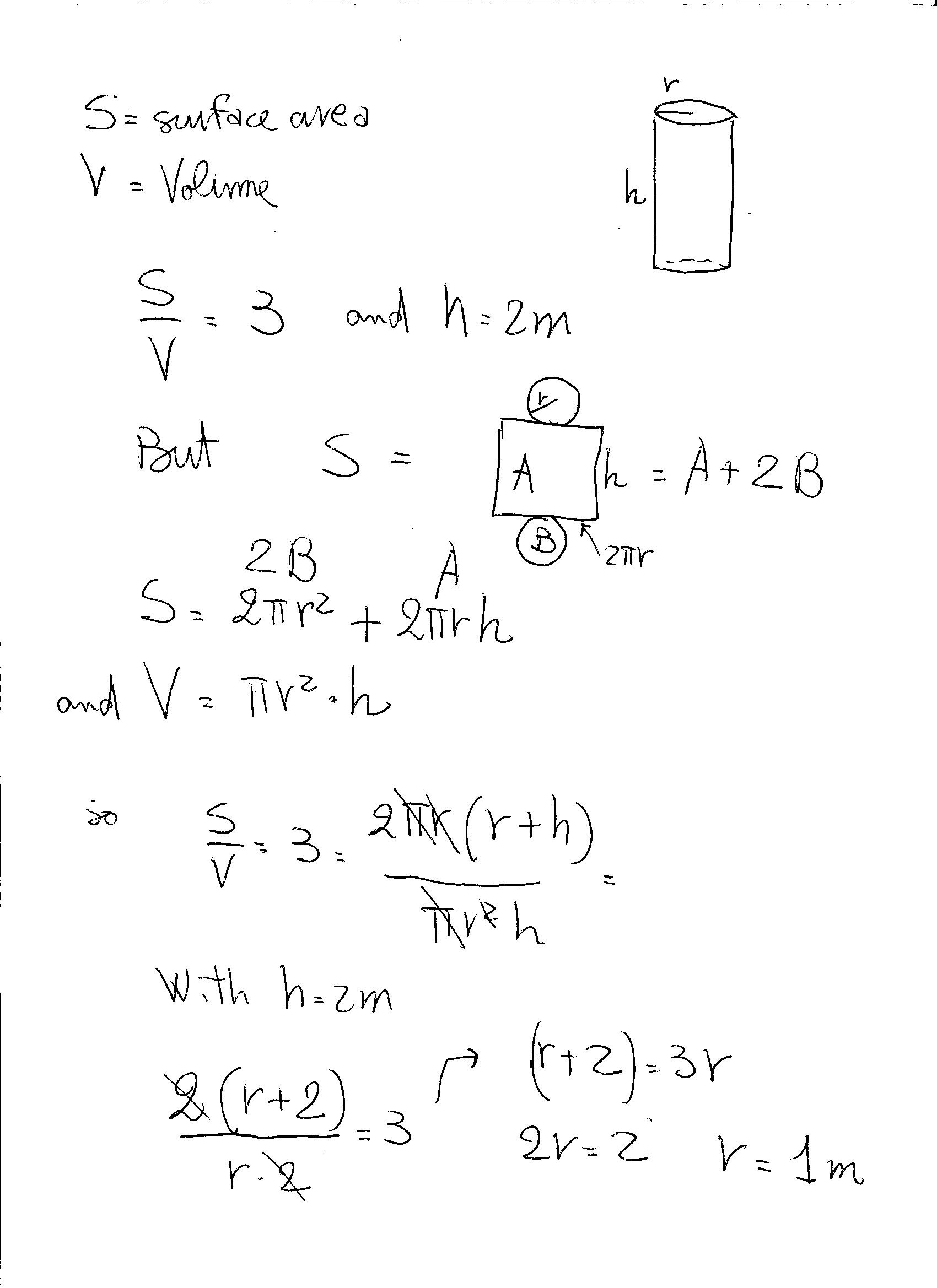
enter image source here

Answer 2 · 2018-05-05T20:33:20

#1#

Consider these formulas: for any cylinder with height #h# and radius #r#, you have:

Surface area: #S = 2pir^2 + 2pi h r = 2pir(r+h)#
Volume: #V = pi hr^2#

We know that #h=2#, so the formulas become

Surface area: #S = 2pir^2 + 2pi * 2* r = 2pir(r+2)#
Volume: #V = 2pir^2#

We also know that

#S/V = \frac{2pir(r+2)}{2pir^2} = \frac{(r+2)}{r} = 3#

Solving for #r# (it is safe to assume that #r ne 0#), we have

#r+2 = 3r \iff 2r = 2 \iff r = 1#

As you can see, the surface area is #6pi#, whereas the volume is #2pi#. The ratio is indeed #3#.