A) Describe the prism. What will be its dimensions? B) What will be its volume?

Genevieve is constructing a rectangular prism with surface area exactly #294m^2#. It will have the greatest possible volume.

1 Answer
Sean
Jan 22, 2018

#A)# In order to maximize Volume, the prism will have to be a cube with side measure of #7#, and the Volume would be:

#B)# #V=lwh=(7)(7)(7)=343# #m^3#

Explanation:

.

Her is a rectangular prism of dimensions Length#=l#, Width#=w#, and Height#=h#:

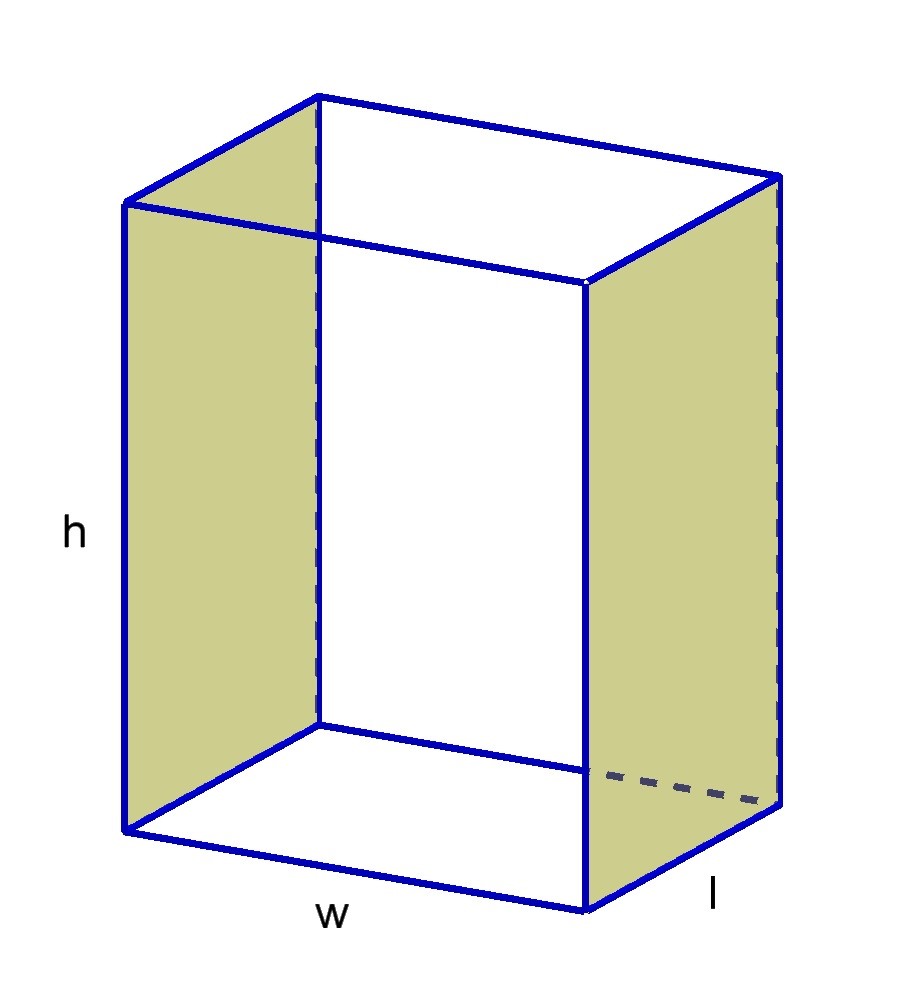
enter image source here

Surface Area#=SA=2lw+2wh+2lh=294# #m^2#

#2(lw+wh+lh)=294#

#lw+wh+lh=147#

#wh+lh=147-lw#

#h(l+w)=147-lw#

We can solve for #h#:

#h=(147-lw)/(l+w)#

Volume#=V=lwh#

Let's plug the value of #h# into the Volume equation:

#V=lw((147-lw)/(l+w))=(147lw-l^2w^2)/(l+w)#

Because we want to maximize the Volume, we need to take its derivative and set it equal to zero to solve for the variable(s) in the equation.

But because the Volume function has two variables, i.e. #l# and #w#, we have to take partial derivatives of it with respect to each variable and set it equal to zero.

First, let's take the partial derivative of #V# with respect to #l# using the Quotient Rule:

#(delV)/(dell)=((147w-2lw^2)(l+w)-(147lw-l^2w^2))/(l+w)^2#

#(delV)/(dell)=(147wl+147w^2-2l^2w^2-2lw^3-147lw+l^2w^2)/(l+w)^2#

#(delV)/(dell)=(cancelcolor(red)(147w)+147w^2-2l^2w^2-2lw^3cancelcolor(red)(-147lw)+l^2w^2)/(l+w)^2#

#(delV)/(dell)=(-l^2w^2+147w^2-2lw^3)/(l+w)^2#

#(delV)/(dell)=w^2/(l+w)^2(147-2lw-l^2)#

Now, let's take the partial derivative of #V# with respect to #w# using the Quotient Rule:

#(delV)/(delw)=((147l-2l^2w)(l+w)-(147lw-l^2w^2))/(l+w)^2#

Simplifying as we did the first partial derivative, we get:

#(delV)/(delw)=l^2/(l+w)^2(147-2lw-w^2)#

Setting these two partial derivatives equal to zero, and knowing that #l# and #w# are non-zero and positive, we have to conclude that:

#147-2lw-l^2=0#

#147-2lw-w^2=0#

Subtracting the second equation from the first, we get:

#147-2lw-l^2-147+2lw+w^2=0#

#-l^2+w^2=0#

#w=+-l#

Since #l# and #w# can only be positive, we have:

#l=w#

We now plug this into the first equation:

#147-2l^2-l^2=0#

#147-3l^2=0#

#l^2=147/3=49#

#l=7#

From above, we have:

#h=(147-lw)/(l+w)=(147-(7)(7))/(7+7)=7#

Therefore, in order to maximize Volume, the prism will have to be a cube with side measure of #7#, and the Volume would be:

#V=lwh=(7)(7)(7)=343# #m^3#

Related questions
Impact of this question
1305 views around the world
You can reuse this answer
Creative Commons License