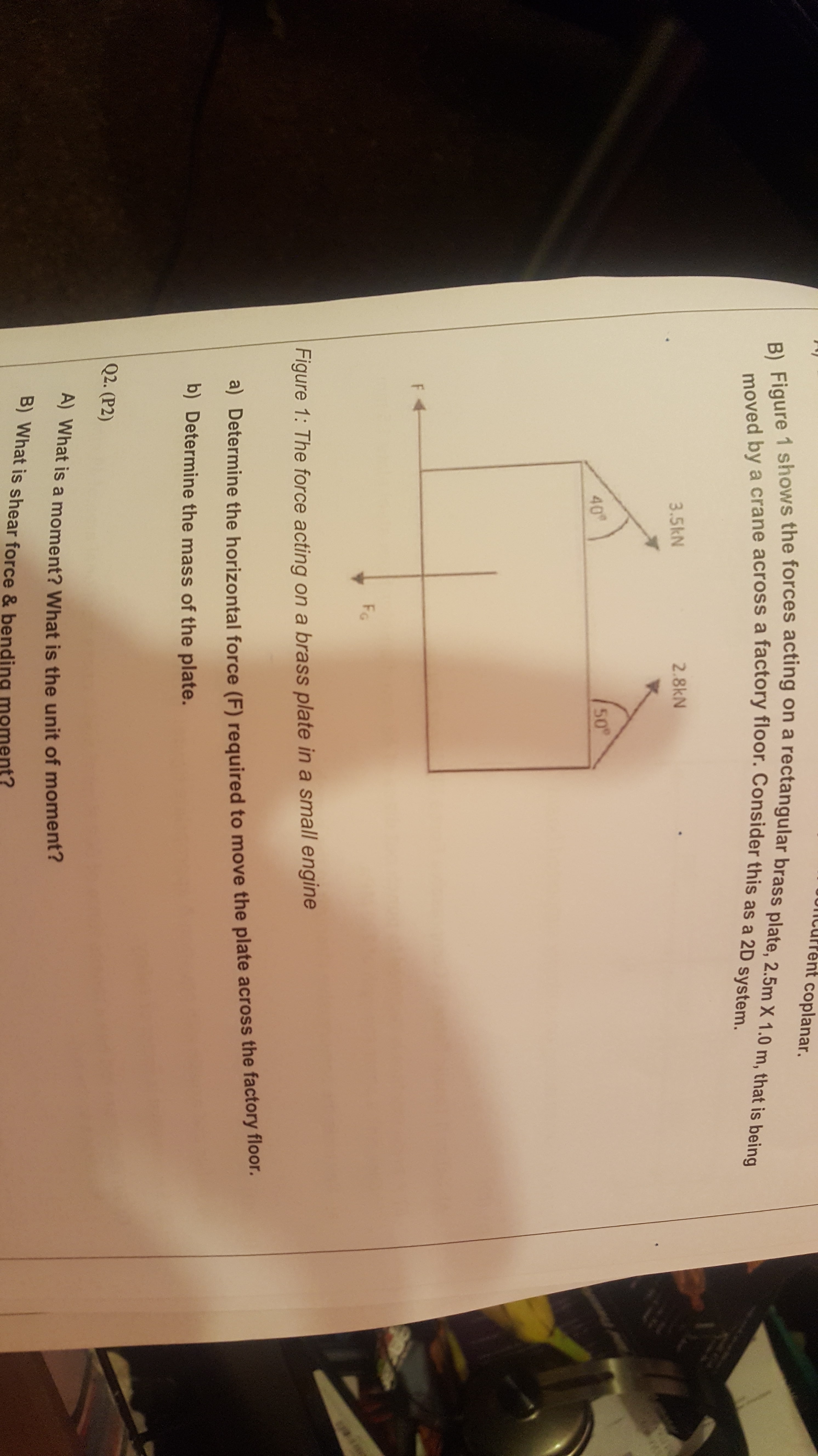
A)Detemine the horizontal force (F) required to move the plate across the factory floor.? b) Determine the mass of the plate?
1 Answer
Mar 21, 2018
See below.
Explanation:
Assuming
1) A coordinate system with origin at the force
2) Brass plate with unknown mass distribution.
Calling
we have
Null force resultant
Null resulting moment regarding point
or equivalently
Solving for

