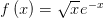Start by calculating the first derivative, the function #f(x)# is the multiplication of #2# functions.
The domain of #f(x)# is #x in [0, +oo)#
Apply the product rule,
#(uv)'=u'v+uv'#
#f'(x)=1/(2sqrtx)*e^-x-e^-xsqrtx=e^-x((1-2x))/(2sqrtx)#
Setting, #f'(x)=0#, gives the critical points
#e^-x((1-2x))/(2sqrtx)=0#, #=>#, #x=1/2#
Build a variation chart
#color(white)(aaaa)##x##color(white)(aaaa)##color(white)(aaaa)##0##color(white)(aaaaaa)##1/2##color(white)(aaaaaaaa)##+oo#
#color(white)(aaaa)##f'(x)##color(white)(aaaaa)####color(white)(a)####color(white)(aa)##+##color(white)(aa)##0##color(white)(aaaaa)##-#
#color(white)(aaaa)##f(x)##color(white)(aaaaa)####color(white)(a)####color(white)(aa)##↗##color(white)(aa)##0.429##color(white)(aa)##↘#
The interval of increasing is #(0,1/2)# and the interval of decreasing is #(1/2,+oo)#
The maximum is at the point #(0.5, 0.429)#
Calculate the second derivative
#f''(x)=-e^-x(1-2x)/(2sqrtx)-e^-x/sqrtx-e^-x(1-2x)/(4x^(3/2))#
#=e^-x(4x^2-4x-1)/(4e^(3/2))#
Setting, #f''(x)=0# gives the inflection points.
#4x^2-4x-1=0#
Solving this quadratic equation
#x=(4+-sqrt((-4)^2-4*(4)*(-1)))/(2*4)=(4+-sqrt32)/(8)#
#x_1=(1+sqrt2)/2=1.21#
#x_2=(1-sqrt2)/2=-0.21#
The inflection point is #(1.21,0.328)#
Make a variation chart to find the concavities
#color(white)(aaaa)##"Interval"##color(white)(aaaa)##(0, 1.21)##color(white)(aaaa)##(1.21, +oo)#
#color(white)(aaaa)##"Sign f''(x)"##color(white)(aaaaa)##-##color(white)(aaaaaaaaa)##+#
#color(white)(aaaa)##"Sign f''(x)"##color(white)(aaaaa)##nn##color(white)(aaaaaaaaa)##uu#
The interval of concave down is #x in (0,1.21)# and the interval of concave up is #x in (1.21, +oo)#
graph{sqrtx e^-x [-0.821, 3.024, -0.854, 1.068]}