A fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is 4/3 and fish is 12 below the surface , find the radius of the circle in cm?
1 Answer
Feb 28, 2018
Explanation:
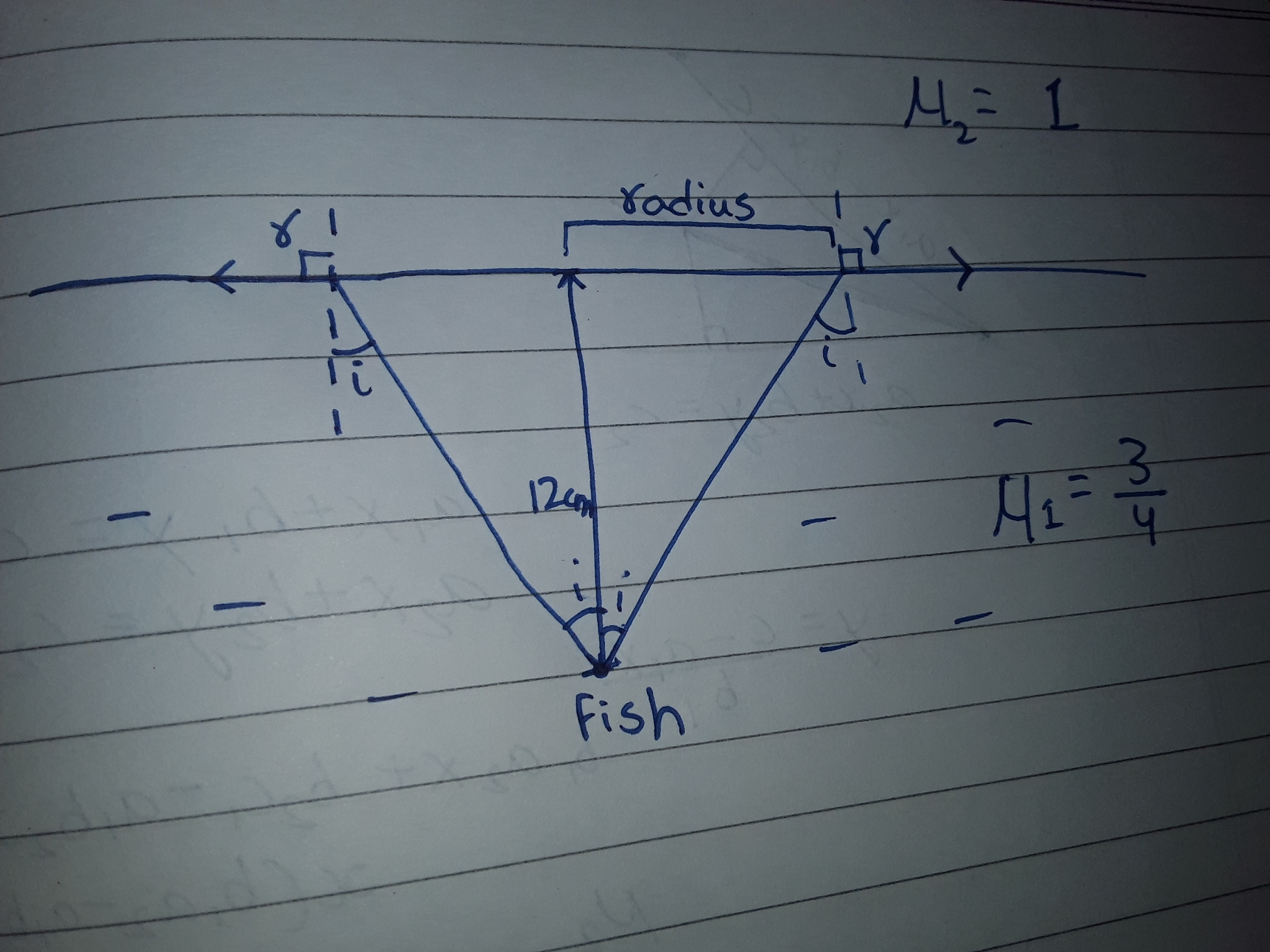
[Note:
If you wonder why there would be circle then try to recall critical angle, if incident angle is beyond that particular angle there would be total internal reflection, so the fish won't be able to see the outside world.
So, as to obtain the radius. We need to take the last light ray into consideration which can enter the eyeball of fish. So, here we'll use critical angle.
Using snell's law
;


