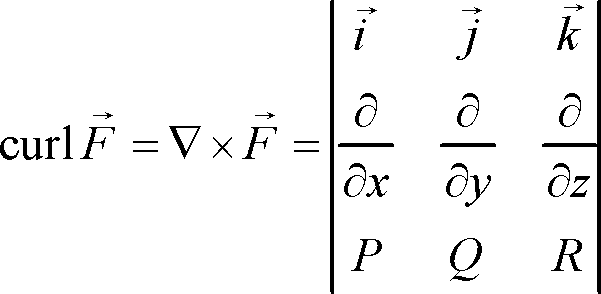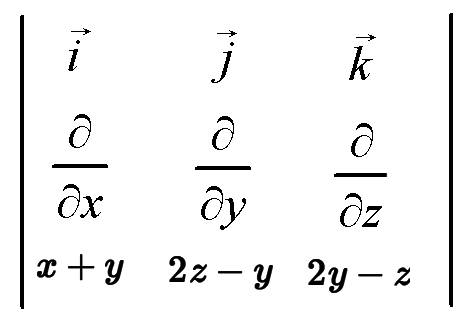If #vecF# is a vector (force) field in #RR^3#, then the curl of #vecF# is the vector #curl(vecF)# and is written as #gradxxvecF#. The vector field #vecF# is conservative iff #curl(vecF)=0#. A curl of zero does not mean that the vector field is definitely conservative, but is the first "pre-requisite." Ultimately, a vector field must have a potential function such as that #vecF=gradf# to be conservative, but if the field has a nonzero curl, it definitely does not have an associated potential function and therefore definitely is not conservative.
As stated above, the curl is given by the cross product of the gradient of #vecF# (in the form #< P, Q, R >#) and itself.
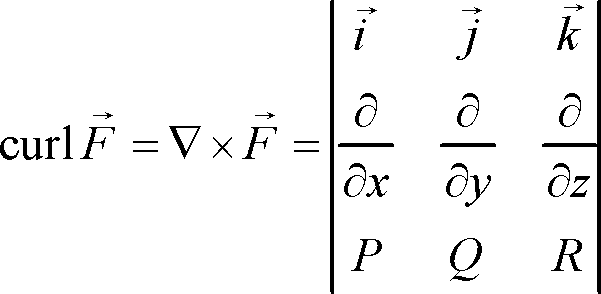
We have #vecF=< x+y, 2z-y, 2y-z ># where
#P=x+y#
#Q=2z-y#
#R=2y-z#
The curl of the vector field is then given as:
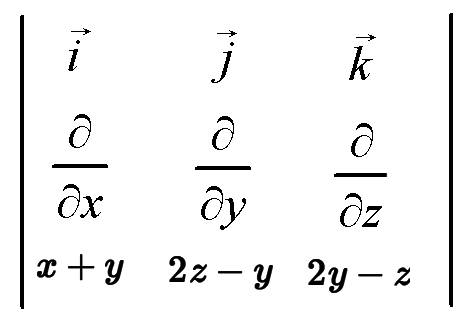
We take the cross product as we usually would, except we'll be taking partial derivatives each time we multiply by a partial differential.
For the #veci# component, we have #del/(dely)(2y-z)-del/(delz)(2z-y)#
#=>(2-2)=0#
For the #vecj# component, we have #del/(delx)(2y-z)-del/(delz)(x+y)#
#=>(0-0)=0#
(Remember that if we take the partial of a function with respect to some variable which is not present, the partial derivative is #0# as we treat all other variables as constants)
Good so far!
For the #veck#component, we have #del/(delx)(2z-y)-del/(dely)(x+y)#
#=>(0-1)=-1#
This gives a final answer of #curl(vecF)=<0,0,-1>!=0#
#:.# Vector field is not conservative