Question

A force field is described by `<F_x,F_y,F_z> = < x , z, y >`. Is this force field conservative?

Answer 1

The force field is conservative; `curl(vecF)=vec0` and `vecF=gradf` for some potential function.

Explanation:

If `vecF` is a vector (force) field in `RR^3`, then the curl of `vecF` is the vector `curl(vecF)` and is written as `gradxxvecF`. The vector field `vecF` is conservative iff `vecF=gradf` for some potential function. If `vecF` is conservative, `curl(vecF)=vec0`. However, this does not mean that a vector field with `curl=vec0` is absolutely conservative; the vector field must also have a potential function to be conservative, but the first prerequisite is that `curl(vecF)=vec0`.

As stated above, the curl is given by the cross product of the gradient of `vecF` (in the form `< P, Q, R >`) and itself.

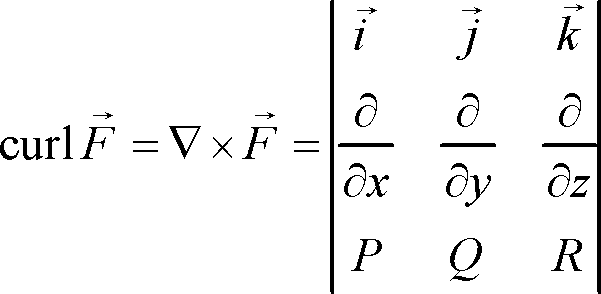
We have `vecF=< x, z, y >` where

`P=x`

`Q=z`

`R=y`

The curl of the vector field is then given as:

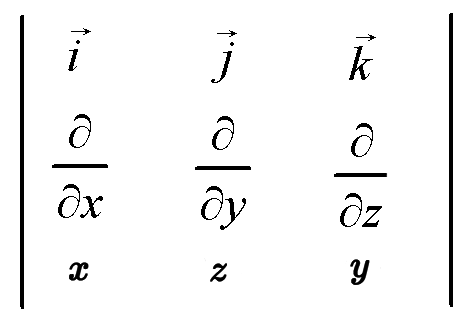
We take the cross product as we usually would, except we'll be taking partial derivatives each time we multiply by a partial differential.

For the `veci` component, we have `del/(dely)(y)-del/(delz)(z)`

`=>(1-1)=0`

For the `vecj` component, we have `del/(delx)(y)-del/(delz)(x)`

`=>(0-0)=0`

(Remember that if we take the partial of a function with respect to some variable which is not present, the partial derivative is `0` as we treat all other variables as constants)

For the `veck`component, we have `del/(delx)(z)-del/(dely)(x)`

`=>(0-0)=0`

This gives a final answer of `curl(vecF)=<0,0,0> =vec0`

This tells that our force field has the potential to be conservative (pun intended). We now must attempt to produce the potential function of the force field. To find the potential function of the vector field, we find `f` so that

`gradf(x,y,z)=< f_x(x,y,z),f_y(x,y,z),f_z(x,y,z) > =vecF(x,y,z)`

We are given `vecF=< x, z, y >`, and so we have:

`f_x(x,y,z)=x`

`f_y(x,y,z)=z`

`f_z(x,y,z)=y`

We now find the antiderivative of one of these components. Which does not matter, so I'll start with `f_x`.

`f_x(x,y,z)=x`

`int(x)dx=1/2x^2+g(y,z)`

(Note we include `g(y,z)` to account for any "constants" which are `y` and `z` variables, since we only integrated with respect to `x`).

`=>f(x,y,z)=1/2x^2+g(y,z)`

We now take the `y` or `z` partial derivative of this answer. Again, it doesn't matter which you start with, so I'll start with `f_y`.

`del/(dely)(1/2x^2+g(y,z))=0+g_y(y,z)`

We set this equal to our original `f_y(x,y,z)` to try to find `g_y(y,z)`

`z=g_y(y,z)`

`=>g(y,z)=zy+h(z)`

Now we take the partial of the above function `f(x,y,z)` with respect to `z`, carrying out the same procedure as we did for `f_y`.

`del/(delz)(zy+h(z))=y+h'(z)`

`=>y=y+h'(z)`

`=>h'(z)=0`

`=>h(z)=0`

Revisiting our function `f(x,y,z)=1/2x^2+g(y,z)`, we now have:

`f=1/2x^2+yz`

We then have satisfied both conditions: `curl(vecF)=0` and a potential function exists.

`:.` Force field is conservative