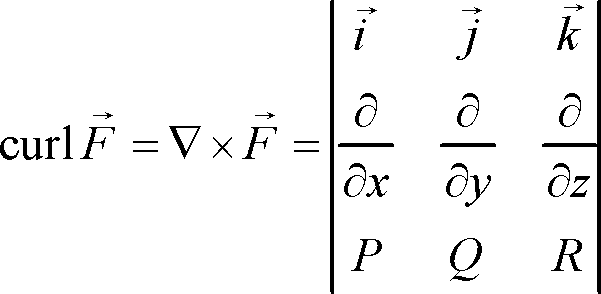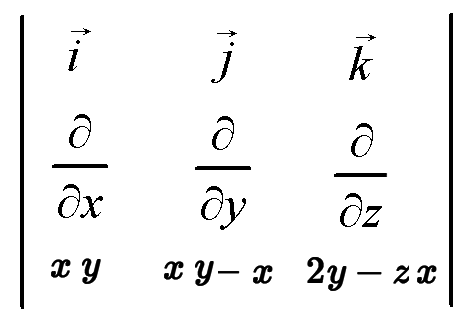If #vecF# is a vector (force) field in #RR^3#, then the curl of #vecF# is the vector #curl(vecF)# and is written as #gradxxvecF#. The vector field #vecF# is conservative iff #vecF=gradf# for some potential function. If #vecF# is conservative, #curl(vecF)=vec0#. However, this does not mean that a vector field with #curl=vec0# is absolutely conservative; the vector field must also have a potential function to be conservative, but the first prerequisite is that #curl(vecF)=vec0#.
As stated above, the curl is given by the cross product of the gradient of #vecF# (in the form #< P, Q, R >#) and itself.
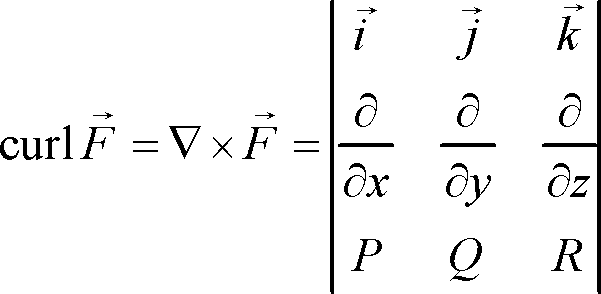
We have #vecF=< xy, xy-x, 2y-zx ># where
#P=xy#
#Q=xy-x#
#R=2y-zx#
The curl of the vector field is then given as:
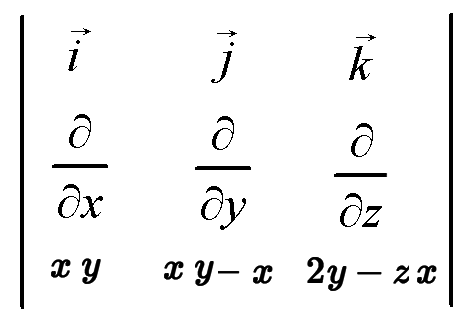
We take the cross product as we usually would, except we'll be taking partial derivatives each time we multiply by a partial differential.
For the #veci# component, we have #del/(dely)(2y-zx)-del/(delz)(xy-x)#
#=>(2-0)=2#
We can tell immediately that the product will not be #vec0#, but we can finish the process.
For the #vecj# component, we have #del/(delx)(2y-zx)-del/(delz)(xy)#
#=>-(-z-0)=z#
(Remember that if we take the partial of a function with respect to some variable which is not present, the partial derivative is #0# as we treat all other variables as constants)
For the #veck#component, we have #del/(delx)(xy-x)-del/(dely)(xy)#
#=>(y-1-x)=y-1-x#
This gives a final answer of #curl(vecF)=<2,z,y-x-1> !=vec0#
#:.# Force field is not conservative