A goat grazes a rectangular paddock 10 metres by 20 metres. It is tethered to the fence at one corner of the paddock by an inextensible rope of length x metres, where 10<x<20? (More in 'details' section).
A goat grazes a rectangular paddock 10 metres by 20 metres. It is tethered to the fence at one corner of the paddock by an inextensible rope of length x metres, where 10<x<20 .
(a) Show that the goat can graze an area of A m^2 , where A=1/2x^2sin^(-1)(10/x)+5sqrt(x^2-100)
(b) If the goat can graze an area equal to half the area of the paddock, find the length of the rope to one decimal place using one application of Newton's method.
Thanks!
A goat grazes a rectangular paddock 10 metres by 20 metres. It is tethered to the fence at one corner of the paddock by an inextensible rope of length
(a) Show that the goat can graze an area of
(b) If the goat can graze an area equal to half the area of the paddock, find the length of the rope to one decimal place using one application of Newton's method.
Thanks!
1 Answer
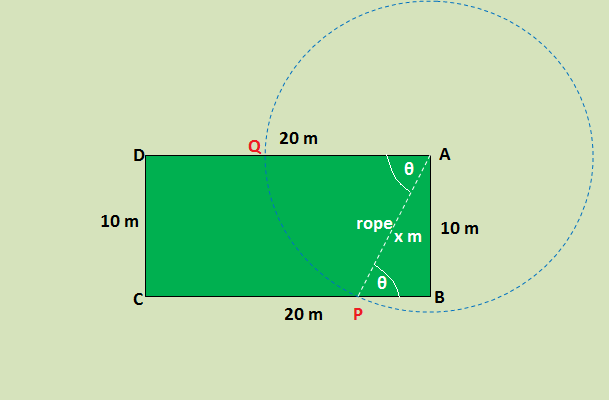 drawn
drawn
Let the rope of length
It is given that
The maximum circular area that the goat can access when it is tethered by an in-extensible rope of length x metre is
(a) The total possible area
(b) If the goat can graze an area equal to half the area of the paddock
The length of the rope to one decimal place calculated using one application of Newton's method will be
This calculation can be done by online calculator .(Link given below)
Taking
and

LINK

