A group of 62 randomly selected students have a mean score of 28.3 on a standardized placement test. The population SD for all students taking the test is #sigma = 3.4#. What is the 90 percent confidence interval for the mean score?
1 Answer
Jul 13, 2016
Population mean is likely to fall between
Explanation:
Given -
#barx=28.3#
#n=62#
#sigma=3.4#
#z# score for 90% confidence interval#1.64#
#SE=sigma/sqrtn=3.4/sqrt62=3.4/7.87=0.43#
90% confidence interval is defined by the formula
#mu=barx+(SExxz)# --------upper limit
#mu=28.3+(0.43 xx 1.64)=28.3+0.705=29.005#
#mu=barx-(SExxz)# --------Lower limit
#mu=28.3-(0.43 xx 1.64)=28.3-0.705=27.595#
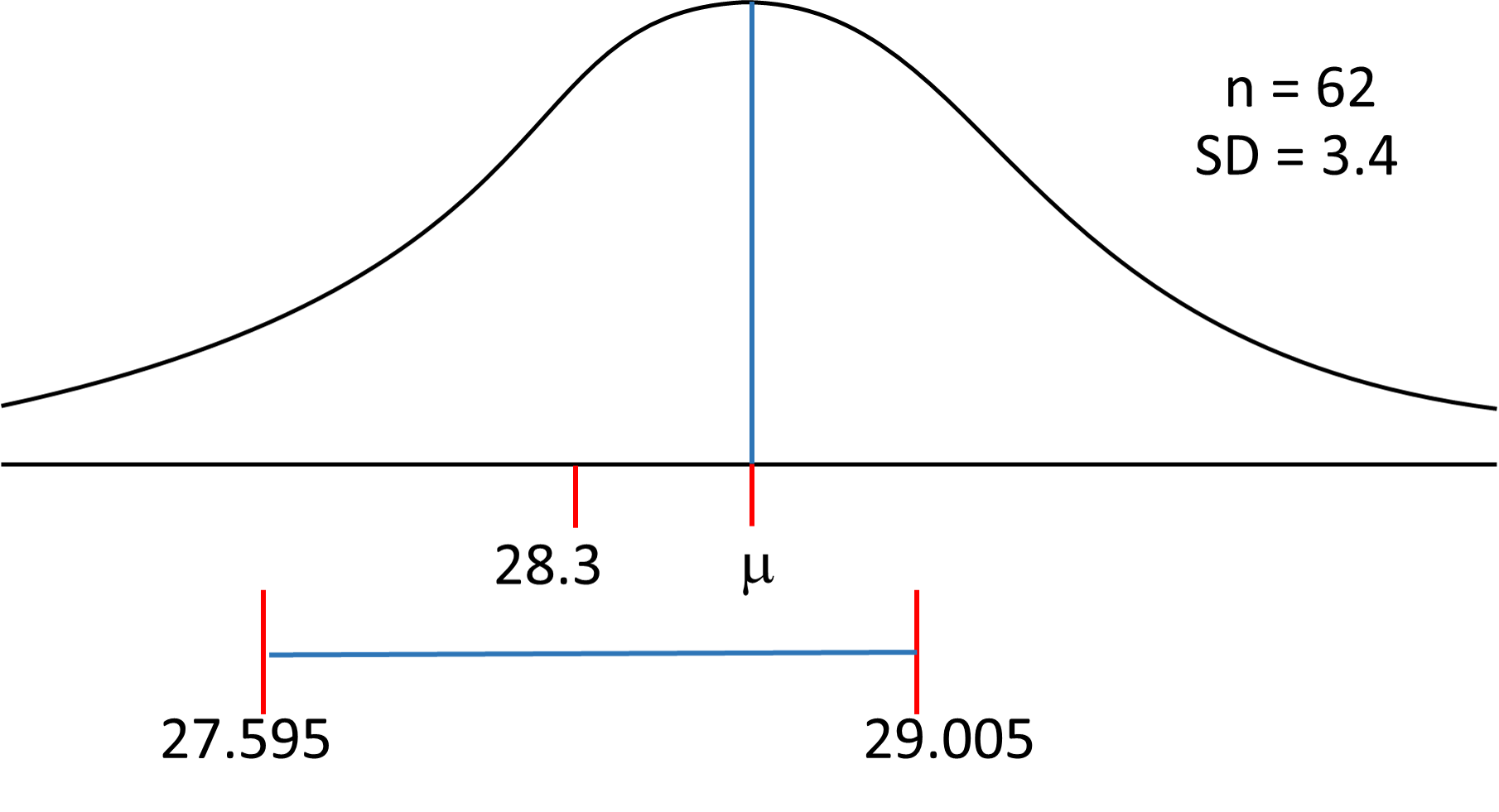
Sample means are normally distributed around the population mean
An interval is developed as

