Question

A hole of radius r is bored through the center of a sphere of radius R. find the volume of the remaining portion of the sphere?

Answer 1

`(4pi)/3 (R^2-r^2)^(3/2)`

Explanation:

We basically are being asked to calculate the volume of a spherical bead, that is, a sphere with a hole drilled through it.

Consider a cross section through the sphere, which we have centred on the origin of a Cartesian coordinate system, and assuming `R gt r`:

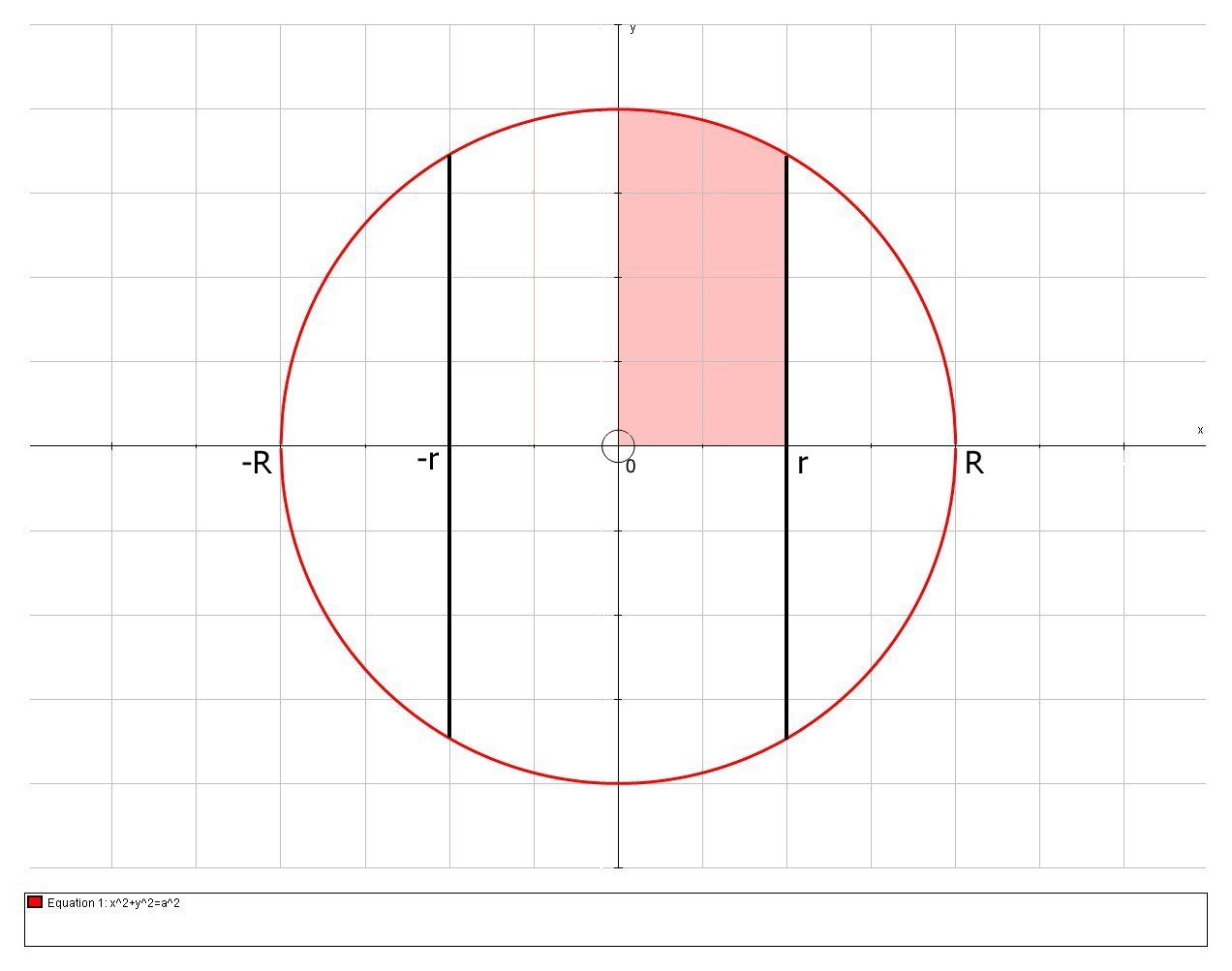
The red circle has radius `R`, hence its equation is:

`x^2+y^2=R^2`

Method 1 - Calculate core and subtract from Sphere

First let us consider the volume of the entire Sphere, which has radius `R`. We use the standard volume formula `V=4/3pir^3`

`:. V_("sphere") = 4/3 pi R^3`

For the bore we can consider a solid of revolution. (Note this is not a cylinder as it has a curved top and bottom from the sphere). We will use the method of cylindrical shells and rotate about `Oy`, the shell formula is:

`V = 2pi \ int_(alpha)^(beta) \ xf(x) \ dx`

Also note that we require twice the volume because we have a symmetrical portion above and below the `x`-axis. The shell volume of revolution about `Oy` for the bore is given by:

`V_("bore") = 2 * 2pi \ int_(0)^(r) \ xsqrt(R^2-x^2) \ dx`

We can evaluate using a substitution:

Let `u=R^2-x^2 => (du)/dx = -2x`
When `{ (x=0), (x=r) :} => { (u=R^2), (u=R^2-r^2) :}`

And so:

`V_("bore") = 4pi \ int_(R^2)^(R^2-r^2) \ (-1/2)sqrt(u) \ du`

`" " = 2pi \ int_(R^2-r^2)^(R^2) \ sqrt(u) \ du`

`" " = 2pi \ [ u^(3/2)/(3/2) ] _(R^2-r^2)^(R^2)`

`" " = (4pi)/3 \ [ u^(3/2) ] _(R^2-r^2)^(R^2)`

`" " = (4pi)/3 \ ((R^2)^(3/2) - (R^2-r^2)^(3/2))`

`" " = (4pi)/3 \ (R^3 - (R^2-r^2)^(3/2))`

`" " = (4pi)/3 R^3 - (4pi)/3 (R^2-r^2)^(3/2)`

And so the total volume is given by:

`V_("total") = V_("sphere") - V_("bore"`
`" " = 4/3 pi R^3 - ( (4pi)/3 R^3 - (4pi)/3 (R^2-r^2)^(3/2))`
`" " = (4pi)/3 (R^2-r^2)^(3/2)`

Method 2 - Calculate volume of bead directly

We can use the same method of a solid of revolution using the method of cylindrical shells and rotate about `Oy`, but this time we will consider the bead itself rather than the core that is removed, again we need twice the volume because we have a symmetrical portion above and below the `x`-axis. The shell volume of revolution about `Oy` for the bead is given by:

`V_("total") = 2 * 2pi \ int_(r)^(R) \ x \ sqrt(R^2-x^2) \ dx`

We can evaluate using a substitution:

Let `u=R^2-x^2 => (du)/dx = -2x`
When `{ (x=r), (x=R) :} => { (u=R^2-r^2), (u=0) :}`

And so:

`V_("total") = 4pi \ int_(R^2-r^2)^(0) \ (-1/2) sqrt(u) \ du`

`" " = 8pi \ int_(0)^(R^2-r^2) \sqrt(u) \ du`

`" " = 8pi \ [ u^(3/2)/(3/2) ] _(0)^(R^2-r^2)`

`" " = (4pi)/3 \ [ u^(3/2) ] _(0)^(R^2-r^2)`

`" " = (4pi)/3 \ ((R^2-r^2)^(3/2) - 0)`

`" " = (4pi)/3 \ (R^2-r^2)^(3/2)`, as above