There is some force of #26.3" N"# acting on the object in the #color(blue)(x)# direction and a frictional force that directly opposes the motion of the box, #f_(k)#. Since the box is not accelerating (constant velocity), there is no net force.
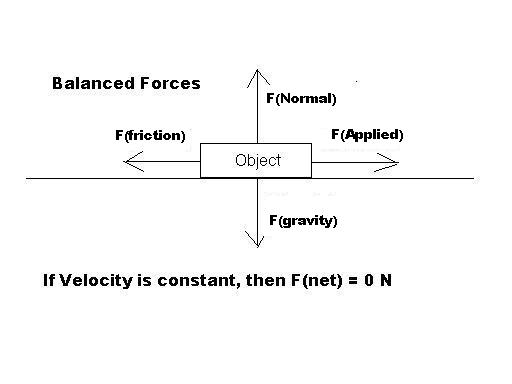
Since we know that the net force is #0#, then we also know that the two opposing forces are equal to each other.
#sumvecF_(x) = ma = 0#
therefore,
#F_(x) = f_(k)#
#26.3 N = f_(k)#
We also know that frictional force is calculated as follows
#f_(k) = mu*N#
Where
#"mu = coefficient of kinetic friction"#
#"N = normal force (N)"#
Knowing this we can rewrite the equation for the forces acting on the box in the #color(blue)(x)# direction as
#color(white)(aaaaaaaaaaaaaaaaaa)color(magenta)(26.3 N = mu*N#
in order to solve for the coefficient of kinetic friction.
But how do we figure out the Normal force?
#---------------------#
See the diagram? Look at the #color(red)(y)# components. The forces acting on the object in the #color(red)(y)# direction are the force of gravity acting downwards and the Normal force acting upwards. Since the object is not accelerating in the #color(red)(y)# direction, we too can set the force of gravity equal to the Normal force.
#F_("gravity") = F_("Normal")#
And since the weight of the object was given to us, we have figured out the Normal force.
#F_("gravity") = F_("Normal")#
#99 N = F_("Normal")#
#---------------------#
Now, back to our original equation that we were working on
#color(white)(aaaaaaaaaaaaaaaaaa)color(magenta)(26.3 N = mu*N#
We can plugin #99 N# for the Normal force and solve for the coefficient of kinetic friction.
#color(magenta)(26.3 N = mu*N#
#(26.3 N)/(99 N)= mu#
#0.27 = mu ("the coefficient of kinetic friction is unitless")#
#color(orange)"Answer: 0.27 = mu"#


