A ladder 5m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4m away from the wall??

Question

36679 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-07-30T13:29:48

The height is decreasing at the rate of #=2.67cms^-1#

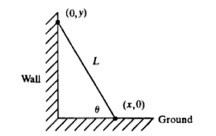
enter image source here

Here , we apply Pythagoras

#x^2+y^2=L^2#

Differentiating with respect to #t#

#2xdx/dt+2ydy/dt=0#

#dx/dt=0.02ms^-1#

#x=4m#

#y=sqrt(5^2-4^2)=sqrt(25-16)=sqrt9=3#

Therefore,

#dy/dt=-x/ydx/dt=-4/3*0.02=-0.0267ms^-1#