A ladder 5m long is standing vertically, flat against a vertical wall, while its lower end in on the horizontal floor. ... Find the speed at which the upper end is moving down the wall 4 seconds after the lower end has left the wall ?
A ladder 5m long is standing vertically, flat against a vertical wall, while its lower end in on the horizontal floor. The lower end moves horizontally away from the wall at a constant speed of 1m/s while the upper end stays in contact with the wall. Find the speed at which the upper end is moving down the wall 4 seconds after the lower end has left the wall.
A ladder 5m long is standing vertically, flat against a vertical wall, while its lower end in on the horizontal floor. The lower end moves horizontally away from the wall at a constant speed of 1m/s while the upper end stays in contact with the wall. Find the speed at which the upper end is moving down the wall 4 seconds after the lower end has left the wall.
1 Answer
Speed is
Explanation:
Using
#{(x_o = 0),(dot x = 1),(y_0 = 5):}#
The relationship between
# x^2 + y^2 = 25#
Differentiate wrt
So speed is
EDIT :
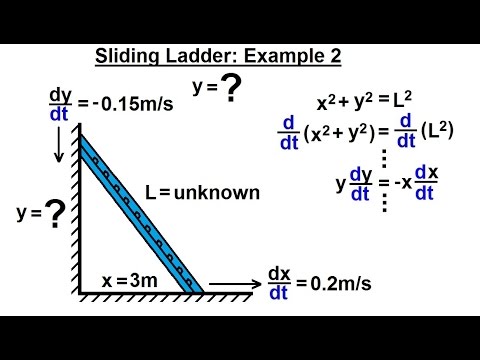
I found this image on YouTube which might help you understand what is going on. NB the numbers are different, but the basic idea is the same: