A light on the ground is 30 feet away from a building. A 4 foot man is walking from the light to the building at a rate of 3 feet per second and is casting a shadow on the building. At what rate is his shadow shrinking when he is 5 feet from the building?

Question

I understand that you have to use similar triangles somehow, but I'm not sure how.

7638 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-15T15:28:47

#sf(-0.58color(white)(x)"ft/s")#

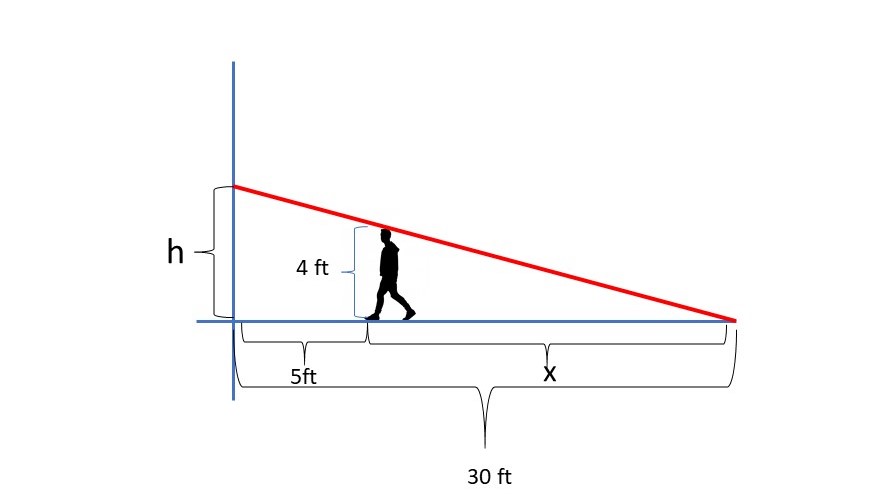
MFDocs

As the man walks towards the building his distance from the lamp x increases as the height of his shadow h decreases.

We can find the relationship between the two by observing the similar triangles. We can say that at any given instant:

#sf(4/x=h/30)#

#:.##sf(h=120/x)#

We are told that:

#sf(dx/dt=3color(white)(x)"ft/s")#

We need to find #sf((dh)/dt)#.

Applying The Chain Rule we get:

#sf((dh)/dt=dx/dtxx(dh)/dx)#

Since #sf(h=120/(x)=120x^(-1))#

Then #sf((dh)/dx=-120x^(-2)=-120/(x^2))#

#:.##sf((dh)/dt=3xx-120/(x^2)=-360/(x^2))#

We need to find the value of #sf((dh)/dt)# when he is 5 ft from the building. This means that the value of x must be 30 - 5 = 25 ft.

#:.##sf((dh)/dt=-360/25^2=-0.58color(white)(x)"ft/s")#