Given points #A(1,2) , B (4,1)#
Reflected across #x = -1#, #y = 3#
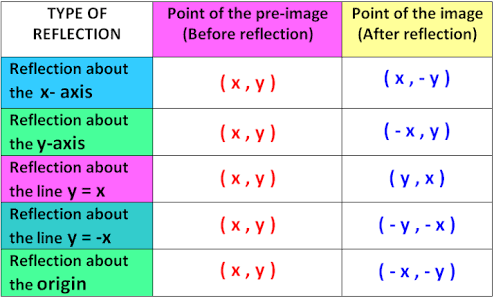
#color(blue)("Reflection Rules :"#
#color(blue)("reflect over x-axis. (x,-y)"#
#color(blue)("reflect over y-axis. (-x,y)"#
#color(blue)("reflect over line y=x. (y,x)"#
#color(blue)("reflect over line y= -x. (-y,-x)"#
#color(blue)("reflect thru origin. (-x,-y)"#
#color(brown)("reflect thru a different point. ex: (5,-1) h=5 k= -1. (2h-x, 2k-y)"#
#color(blue)("reflect over a line. ex: x=6. (2h-x, y)"#
#color(blue)("reflect over a line. ex: y= -3. (x, 2k-y)"#
#A (x,y) -> A’(x, y) = (1,2) -> ((2x’- 1), (2y’ - 2))#
#A’(x,y) => ((-2 - 1), (6 - 2)) => (-3, 4)#
#B (x,y) - > B’ (x,y) = (4 , 1) -> ((2x’ - 4), (2y’ - 1) #
#B’(x,y) => ((-2 - 4), (6 - 1) => (-6, 5)#
New coordinates after reflection are #A’(-3, 4), B’(-6, 5)#
Now we we have to find A”, B” after rotation about point C (2,2) with a dilation factor of 3.
#A”(x, y) -> 3 * A’(x,y) - C (x,y)#
#A”((x),(y)) = 3 * ((-3), (4)) - ((2), (2)) = ((-11),(10))#
Similarly, #B”((x),(y)) = 2 * ((-6), (5)) - ((2), (2)) = ((-14),(8))#
New endpoints are #A”(-11, 10), B”(-14, 8)#
Distance of new points from origin
#vec(OA”) = sqrt(-11^2 + 10^2) ~~ 14.87#
#vec(OB”) = sqrt(-14^2 + 8^2) ~~ 16.12#

