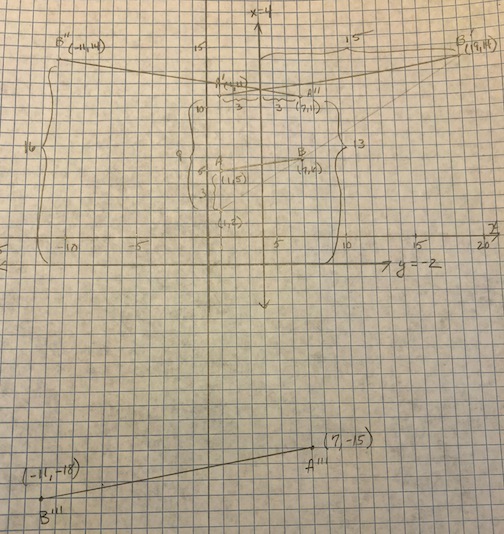
Given: #A(1, 5), B(7,6)#. Line #bar (AB)# is dilated about #(1,2)# by a factor #k = 3#. Then the line segment is reflected across #x = 4# and #y = -2#.
Dilated about #(1,2)# . Find the distance to each endpoint from the dilated point:
#d_(A to (1,2)) = sqrt((5-2)^2 + (1-1)^2) = sqrt(9) = 3#
#d_(B to (1,2)) = sqrt((6-2)^2 + (7-1)^2) = sqrt(16+36) = sqrt(52) = 2sqrt(13)#
Triple the distance (dilate the length to the point #(1, 2)):#
#3(3) = 9; " " 3*sqrt(52) = 3sqrt(52) = 6sqrt(13)#
Since #(1,2)# & #(1,5)# have the same #x# value, the dilated point has the same #x# value:
#" "A'(1, 2+9) = A'(1, 11)#
The 2 is added from the dilated point's #y# value.
Use proportions to find the #B'(x_B, y_B)# coordinates:
#(2sqrt(13))/(6sqrt(13)) = 6/x; " "2sqrt(13)x = 36 sqrt(13); " "x = (36 sqrt(13))/(2 sqrt(13)) = 18#
#x_B = 1 + 18 = 19#
The 1 is added from the dilated point's #x# value.
#(2sqrt(13))/(6sqrt(13)) = 4/y; " "2sqrt(13)y = 24 sqrt(13); " "y = (24 sqrt(13))/(2 sqrt(13)) = 12#
#y_B = 2 + 12 = 14#
The 2 is added from the dilated point's #y# value.
Dilated line segment points: #" "A'(1, 11); " "B'(19, 14)#
Reflected about the #x = 4# line:
#x# distance from #x = 4# to #x_(A') = 3#
#x# distance from #x = 4# to #x_(B') = 15#
Since the points are on opposite sides of #x = 4# there are two coordinate rules:
coordinate rule of reflected point A' :#(x, y) -> ( 4+x"-distance", y)#
coordinate rule of reflected point B' :#(x, y) -> (4 - x"-distance", y)#
#A''(4+3, 11) = (7, 11)#
#B''(4 - 15, 14) = (-11, 14)#
Reflected about #x = 4# line segment points: #A'(7, 11); " "B'(-11, 14)#
Reflected about the #y = -2# line:
#y# distance from #y = 2# to #y_(A'') = 13#
#y# distance from #y = 2# to #y_(B'') = 16#
coordinate rule of reflected points :#(x, y) -> ( x, -2 - y "-distance")#
#A'''(7, -2 - 13) = (7, -15)#
#B'''(-11, -2 - 16) = (-11, -18)#
Reflected about #y = -2# line segment points: #A'(7, -15); " "B'(-11, -18)#
distance of each endpoint from the origin:
#d_(A''' to (0,0))= sqrt(7^2 + (-15)^2) = sqrt(274)~~16.6#
#d_(B''' to (0,0)) = sqrt((-11)^2 + (-18)^2) = sqrt(445)~~21.1#