Question

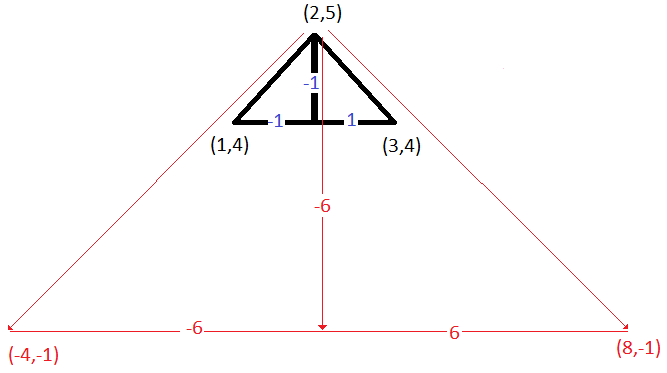
A line segment has endpoints at `(1 ,4 )` and `(3 ,4 )`. The line segment is dilated by a factor of `6` around `(2 ,5 )`. What are the new endpoints and length of the line segment?

Answer 1

New endpoints: `(-4,-1), (8,-1)`
New line segment length: `12`

Explanation:

Note that the distance between the initial line segment end points: `(1,4)` and `(3,4)` is `color(green)(2)` units.
Dilating by a factor of `color(magenta)6` will result in a new length of `color(magenta)6xxcolor(green)2=color(red)(12)`

Consider the vectors from the point of dilation: `(2,5)` and each of the end points:
#{: ("Initial endpoints:",color(white)("xxx"),(1,4),color(white)("xxx"),(3,4)), ("vector from dilation point "(2,5)":",color(white)("xxx"),(-1,-1),color(white)("xxx"),(1,-1)), ("vector after dilation " 6xx":"color(white)("xxx"),,(-6,-6),color(white)("xxx"),(6,-6)), ("new end points:",color(white)("xxx"),(2,5)+(-6,-6),color(white)("xxx"),(2,5)+(6,-6)), (,color(white)("xxx"),=color(red)(""(-4,-1)),color(white)("xxx"),=color(red)(""(8,-1))) :}#