A line segment has endpoints at #(1 ,9 )# and #(6 ,7 )#. The line segment is dilated by a factor of #4 # around #(4 ,3 )#. What are the new endpoints and length of the line segment?

Question

1381 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-02T20:49:55

#"the new end points of line segment are:(-8,27),(12,19)"#
#"the length of line segment is :"sqrt 464#

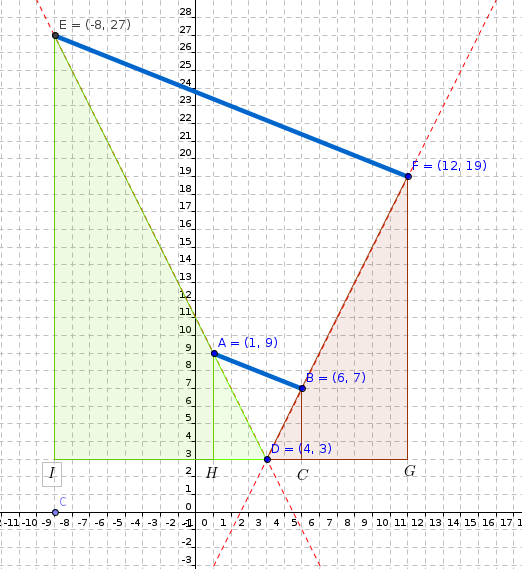
enter image source here
#"the point of D(4,3) is dilatation point"#

#"the point F is image of B"#

#"distance between BC is :"7-3=4#

#"distance between FG is :"4*"factor"=4*4=16#

#"y coordinate of F is :" 3+16=19#

#"distance between DC is :"6-4=2#

#"distance between DG is :"2*"factor"=2*4=8 #

#"x coordinate of F is :"4+8=12#

#"coordinates of F are :"F(12,19)#

#"The point of E is image of A"#

#"distance between AH is:"9-3=6#

#"distance between EI is:"6*"factor"=6*4=24#

#"y coordinate of E is :"3+24=27#

#"distance between HD is :"4-1=3#

#"distance between ID is :"3*"factor"=3*4=12#

#"the x coordinate of E is :"4-12=-8#

#"coordinates of E are :"E(-8,27)#

#"length of line segment AB :"#

#bar (AB)=sqrt((6-1)^2+(7-9)^2)#

#bar (AB)=sqrt(25+4)=sqrt(29)#

#"length of line segment EF:"#

#bar (EF)=sqrt((12+8)^2)+(19-27)^2#

#bar (EF)=sqrt(400+64)=sqrt(464)#