A line segment has endpoints at #(3 ,2 )# and #(5 ,4 )#. The line segment is dilated by a factor of #4 # around #(2 ,3 )#. What are the new endpoints and length of the line segment?
2 Answers
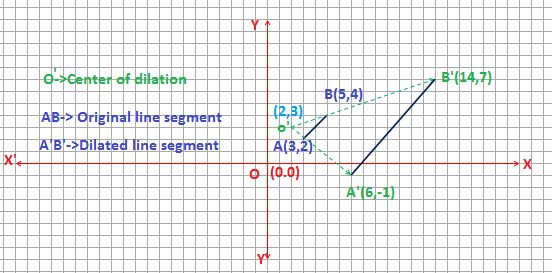
We know,if a point P of coordinate (a,b) be dilated by a factor n around the point of coordinate (h,k), then after dilation the new position of point will be
This means
Using this formula we get
Length of
Length of
length =
Explanation:
If
so if
and


