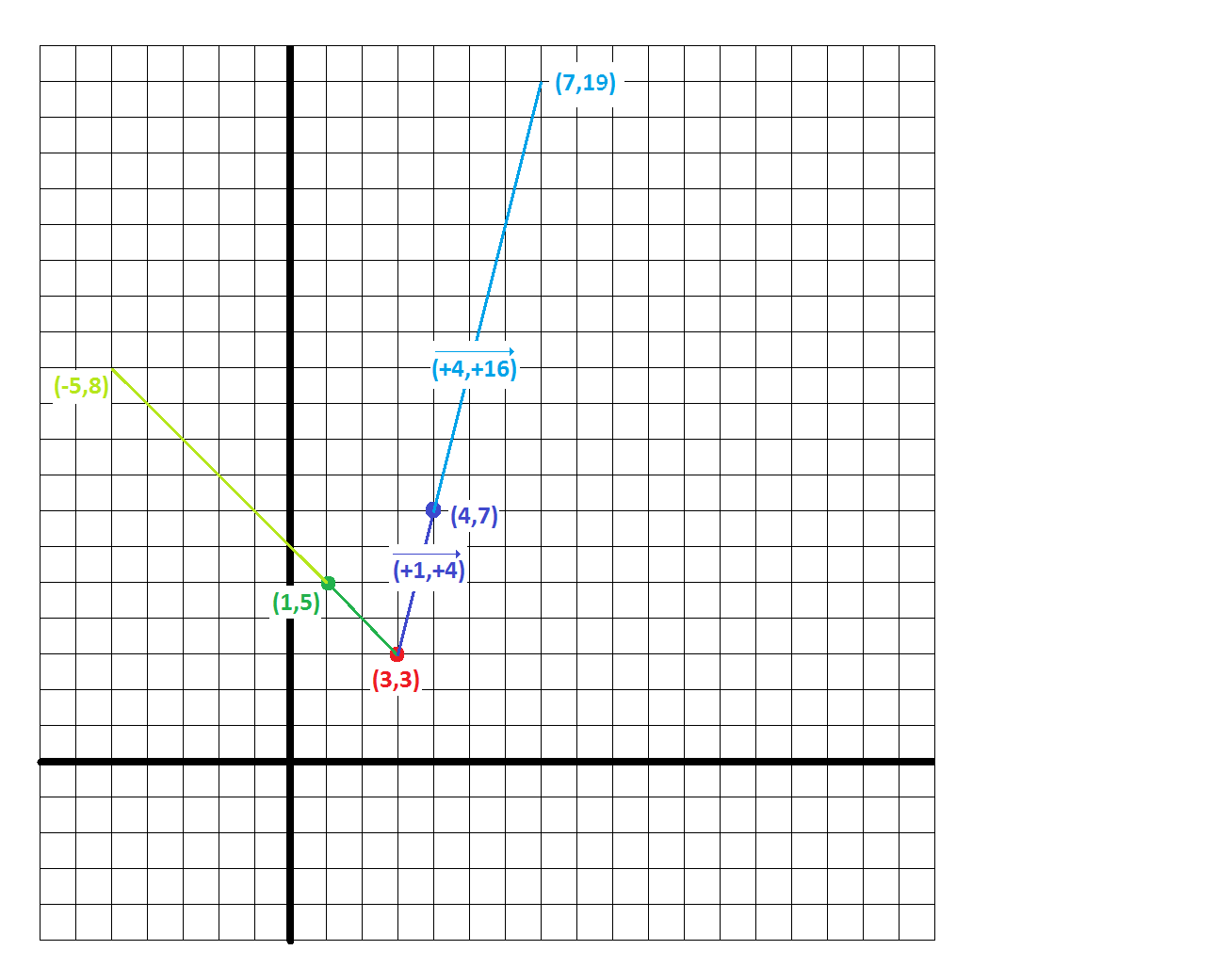
A line segment has endpoints at #(4 ,7 )# and #(1 ,5 )#. The line segment is dilated by a factor of #4 # around #(3 ,3 )#. What are the new endpoints and length of the line segment?
1 Answer
New endpoints:
New line segment length:
Explanation:
Dilation about a center means that all points are moved so that the distance from the center is increased by the dilation factor along the same vector.
By saying "along the same vector" we mean that the slope:
In this example the center is at
scaling this up by the dilation factor of
gives a new offset from the center of
for a resulting location:
Similarly, we can determine the dilated location of
and the length of the dilated line segment is simply the distance between the dilated endpoints