A line segment has endpoints at #(7 ,6 )# and #(9 ,2 )#. The line segment is dilated by a factor of #4 # around #(4 ,3 )#. What are the new endpoints and length of the line segment?

Question

1746 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-16T13:30:38

#"please have a look the animation below"#

#"The new end points of line segment are :"F(16,15),I(24,-1)#

#"Length of the line segment is :"17.89#

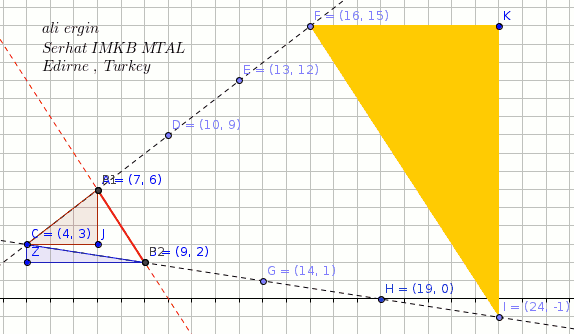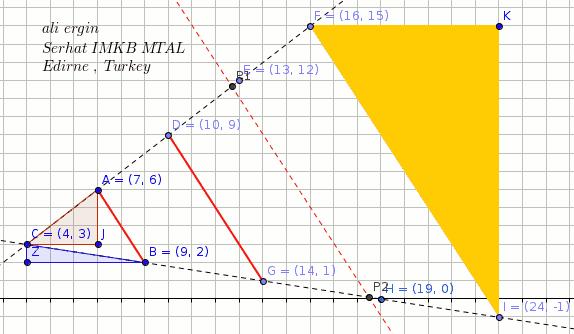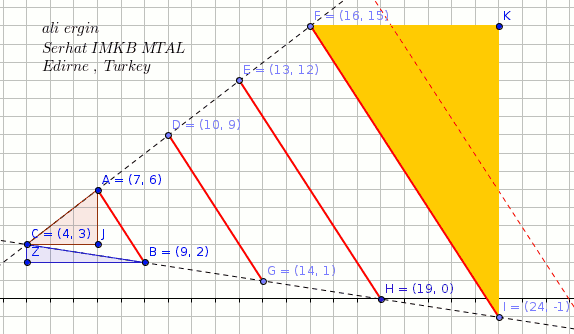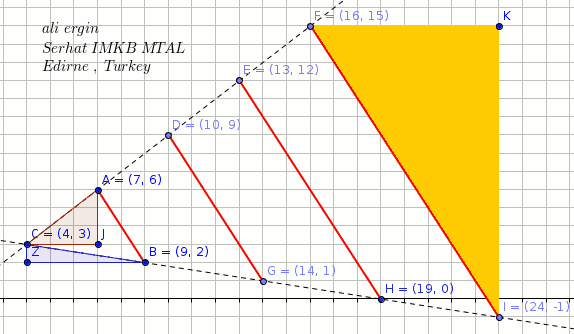
enter image source here

#"the coordinates of point F:"#

#CJ*"factor"=3*4=12#

#4+12=16" the x coordinate of F"#

#AJ*"factor"=3*4=12#

#3+12=15"the y coordinate of F"#

#F(16,15)#

#"the coordinates of I Point:"#

#ZB*"factor"=5*4=20#

#4+20=24" the x coordinate of I"#

#CZ*"factor"=1*4=4#

#3-4=-1" the y coordinate of I")#

#I=(24,-1)#

#"the length of line segment FI :"#

FI=sqrt((16-24)^2+(15+1)^2)

#FI=sqrt(64+256)#

#FI=sqrt(320)#

#FI=17.89#