Question

A line segment has endpoints at `(9 ,1 )` and `(1 ,2 )`. The line segment is dilated by a factor of `4` around `(3 ,3 )`. What are the new endpoints and length of the line segment?

Answer 1

The new endpoints are `A'(x_a', y_a')=(27, -5)` and `B'(x_b', y_b')=(-5, -1)`

Explanation:

Let `A(x_a, y_a)=(9, 1)` and `B(x_b, y_b)=(1, 2)`

Dilated by a factor of `4`

Let `A'(x_a', y_a')` and
Let `B'(x_b', y_b')` be the new points

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let us solve the new point `A'(x_a', y_a')`

Working equation to solve `x_a'`

`(x_a'-3)/(x_a-3)=4/1`

`(x_a'-3)/(9-3)=4/1`

`(x_a'-3)/6=4`

`x_a'=27`

Working equation to solve `y_a'`

`(y_a'-3)/(y_a-3)=4/1`

`(y_a'-3)/(1-3)=4/1`

`(y_a'-3)/(-2)=4`

`y_a'=-5`

the new point `A'(x_a', y_a')=(27, -5)`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let us solve the new point `B'(x_b', y_b')`

Working equation to solve `x_b'`

`(x_b'-3)/(x_b-3)=4/1`

`(x_b'-3)/(1-3)=4/1`

`(x_b'-3)/-2=4`

`x_b'=-5`

Working equation to solve `y_b'`

`(y_b'-3)/(y_b-3)=4/1`

`(y_b'-3)/(2-3)=4/1`

`(y_b'-3)/(-1)=4`

`y_b'=-1`

the new point `B'(x_b', y_b')=(-5, -1)`

Kindly see the graph of the segments

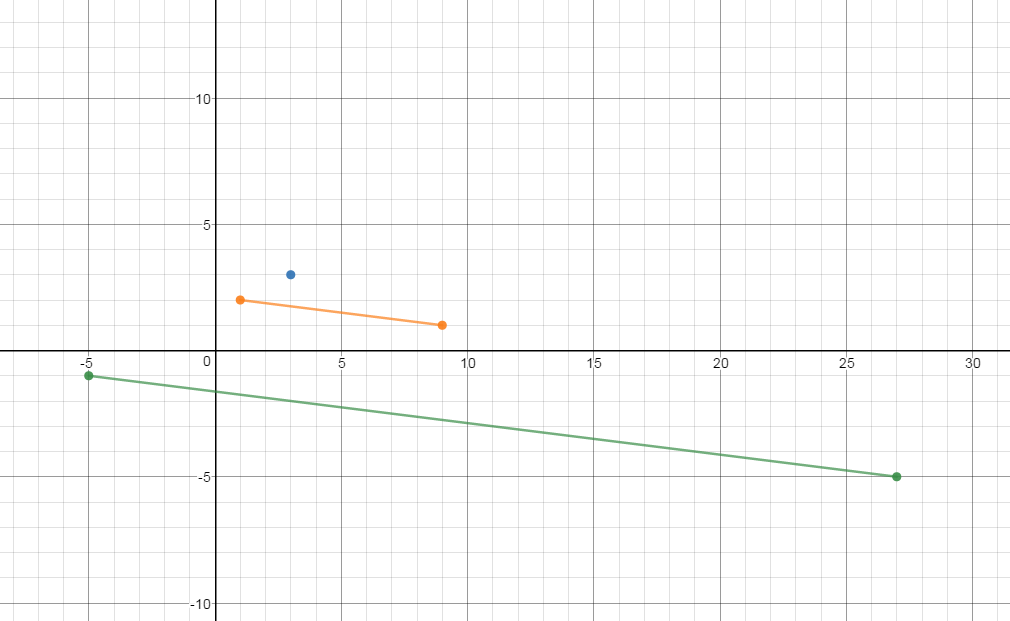
God bless....I hope the explanation is useful.