A line segment has endpoints at #(9 ,7 )# and #(1 ,2 )#. The line segment is dilated by a factor of #4 # around #(3 ,3 )#. What are the new endpoints and length of the line segment?

Question

1345 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-17T14:25:03

#color(blue)((27,19) \ \ "and" \ \(-5,-1)#

One method to perform these is by using vectors.

Let:

#bba# be position vector #((9),(7))#

#bb(b)# be position vector #((1),(2))#

#bbd# be position vector #((3),(3))#

#vec(bb(da))=((6),(4))#

Dilations by a factor 4:

#4vec(bb(da))=4((6),(4))=((24),(16))#

Position vector of the image of #bba#:

We now just add:

#a'=bbd+4vec(bb(da))=((3),(3))+4((6),(4))=((27),(19))#

#:.#

#(9,7)->(27,19)#

We do the same for point b:

#vec(bb(db))=((-2),(-1))#

Position vector of the image of #bb(b)#

#bb(b)+4vec(bb(db))=((3),(3))+4((-2),(-1))=((-5),(-1))#

#(1,2)->(-5,-1)#

So new endpoints are:

#(27,19),(-5,-1)#

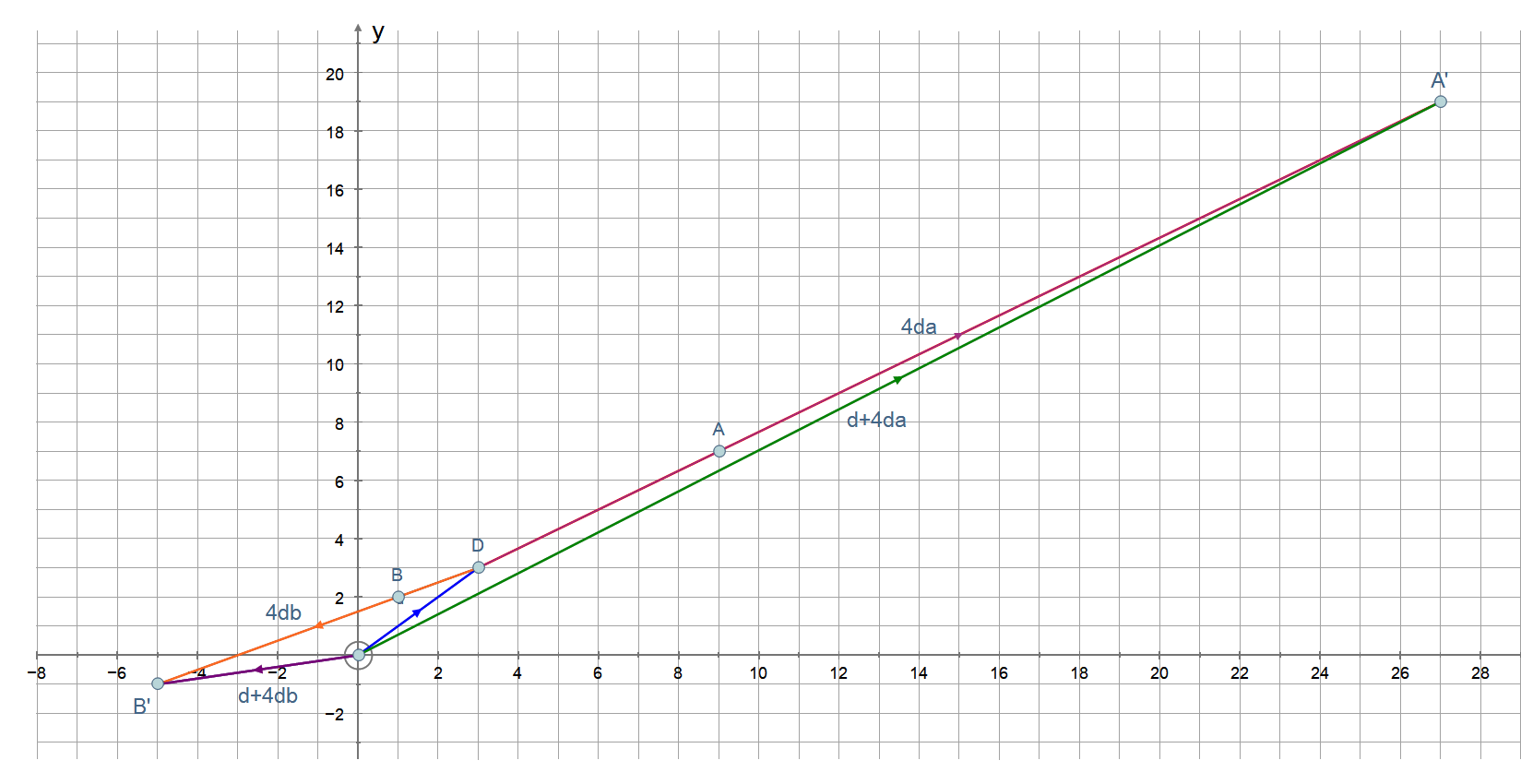
PLOT:

enter image source here