A line segment is bisected by a line with the equation # - 2 y - x = 1 #. If one end of the line segment is at #( 8 , 3 )#, where is the other end?
1 Answer
Explanation:
Consider a horizontal line segment from
with a total length twice that of the horizontal distance from
From the diagram below we can see that this horizontal line will intersect
and will have its left-most end at
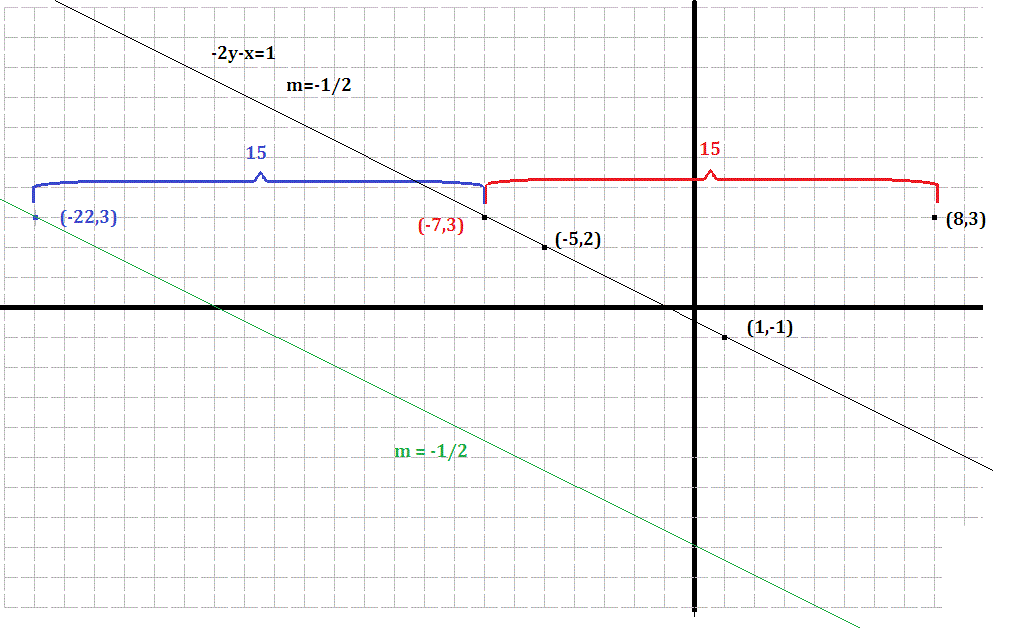
Obviously this horizontal line is bisected by
Consider a line through this left-most point with the same slope as
Using the slope-point form we can see that the equation of this line can be written as
Assertion
for any point
This Assertion follows immediately from considering a modified version of the above diagram.
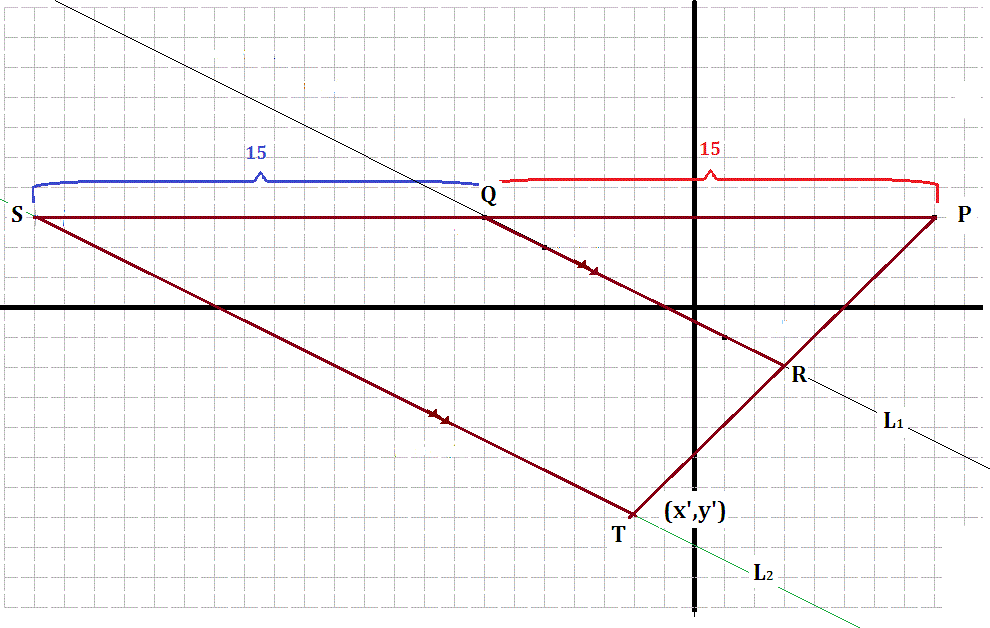
Since
