Question

A line segment is bisected by a line with the equation `2 y + x = 7`. If one end of the line segment is at `( 5 , 3 )`, where is the other end?

Answer 1

`Q=(17/5, -1/5)`

Explanation:

First off, even if it is crude, draw a sketch.

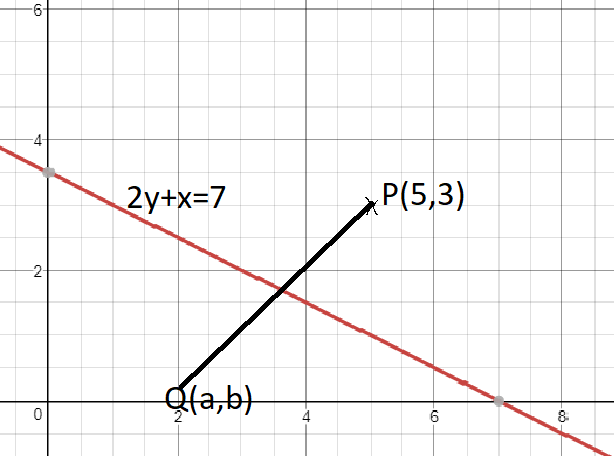
If the bisectors are perpendicular, then the products of their gradients will be `-1`

Let `L` be `2y+x=7`
`y=-1/2x+7/2`
I will be using `m` to denote the gradient (its easier than writing grad for formatting)
`:.m_L=-1/2`
Let `B=`bisector
`m_B*m_L=-1`
`:.m_B=2`

Now, we are searching for the equation of a line given a gradient and a point. This will allow us to easily find points on the bisector. We will use:

`y-y_1=m(x-x_1)` where `(x_1,y_1)` is a co-ordinate and `m` is the gradient.

`:.` eqn of B;

`y-3=2(x-5)`
`y-3=2x-10`
`y=2x-7`

Going back to our sketch, there is a point that these two lines cross. We can find this point by solving simultaneously for B and L

Subst B into L

`2(2x-7)+x=7`
`5x-14=7`
`5x=21`
`x=21/5`

`y=2x-7`
`y=2*21/5-7`
`y=7/5`

Let `M=(21/5, 7/5)`

We can now use column vectors to get us to Q. Since the part of the segment either side of the line bisecting it is equal, we know that the vector `vec(PM)=vec(MQ)`

`vec(PM)=((21/5-5),(7/5-3))`
`=((-4/5),(-8/5))`
`:.vec(MQ)=((-4/5),(-8/5))`
`Q=(21/5-4/5, 7/5-8/5)`
`Q=(17/5, -1/5)`

There is quite probably a simpler way to do this, but I don't know of any. Please tell me if I need to clarify anything