A line segment is bisected by a line with the equation # - 3 y + 6 x = 5 #. If one end of the line segment is at #( 3 , 3 )#, where is the other end?

1 Answer
Alan P.
Oct 18, 2016

The other end will be any point on the line
#color(white)("XXX")-3y+6x=1#

Explanation:

To find one point that satisfy the required conditions, we could take the horizontal line through #(3,3)# and note that it intersects the given bisector equation at #(7/3,3)#

#(7/3,3)# is #2/3# to the left of #(3,3)#
The point horizontally #2/3# further to the left of #(7/3,3)#
is #(5/3,3)#

The bisector line, #-3y+6x=5# bisects the line segment between #(3,3)# and #(5/3,3)#
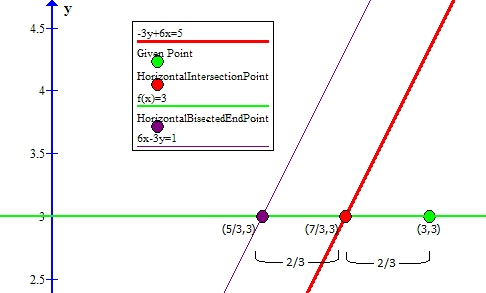
enter image source here

Furthermore any point, #P# on the line through #(5/3,3)# and parallel to the bisector line #-3y+6x=5#
will provide an endpoint that meets the requirement.
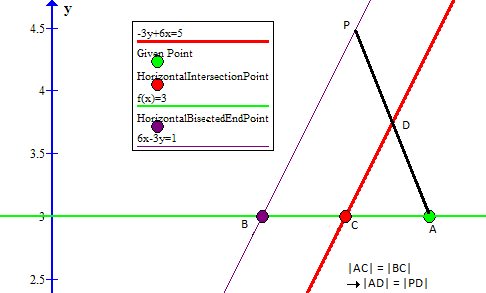
enter image source here

#-3y+6x=5# has a slope of #3#
So the required line will have a slope of #3# and pass through #(5/3,3)#
Using the slope-point form and then manipulating the derived equation into a similar form to that of the bisector line,
we get #-3y+6x=1#

Related questions
See all questions in Perpendicular Bisectors
Impact of this question
1493 views around the world
You can reuse this answer
Creative Commons License