Question

A line segment is bisected by a line with the equation `- 3 y + 6 x = 6`. If one end of the line segment is at `( 3 , 3 )`, where is the other end?

Answer 1

The other end could be any point on the line `y=2x-1`

Explanation:

For convenience, I will rearrange the given equation
`color(white)("XXX")-3y+6x=6`
as
`color(white)("XXX")y=2x-2`

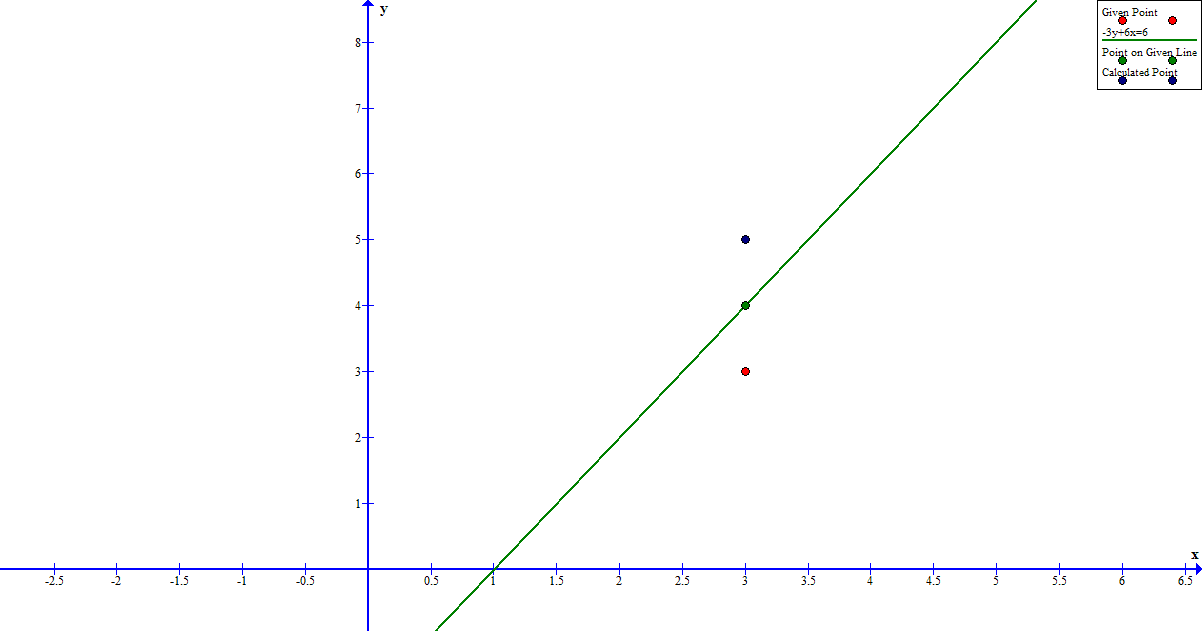
Consider the vertical line through `(3,3)`.
Since `x` is constant for all points on a vertical line,
this vertical line will intersect `y=2x-2` at `(3,4)`

The distance between `(3,3)` and `(3,4)` is `1` unit.

The point `(3,5)` is also on this vertical line at a distance of `2` units from `(3,3)`.

Therefore `y=2x-2` (originally given as `-3y+6x=6`) bisects the line segment joining `(3,3)` and `(3,5)`.

Therefore one possible endpoint would be at `(3,5)`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Perhaps less obviously, any point on a line through `(3,5)` and parallel to the given line `y=2x-2` (or in its original but less convenient form `-3y+6x=6`)
will also be a line segment endpoint bisected by the given equation.

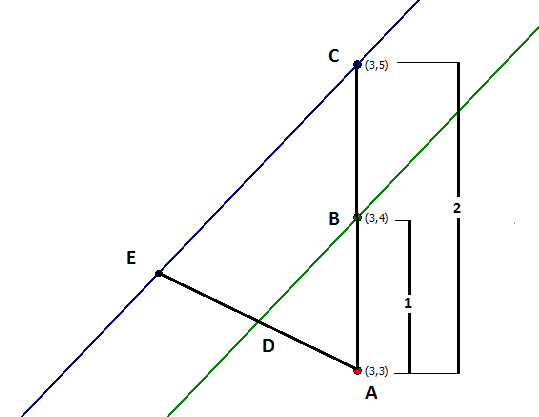
From the image above we can see that for an arbitrary point `E` on a line parallel to the given bisector line
`triangle ABD ~ triangle ACE`
and since `abs(AB)=1/2abs(AC)`
`rarr abs(AD)=1/2abs(AE)`
(i.e. the given line is a bisector for `AE`)

Since `y=2x-2` has a slope of `2`
the line parallel to it and through `(3,5)` will also have a slope of `2`
and using the slope-point form:
`color(white)("XXX")y-5=2(x-3)`
Which can be simplified as
`color(white)("XXX")y=2x-1`