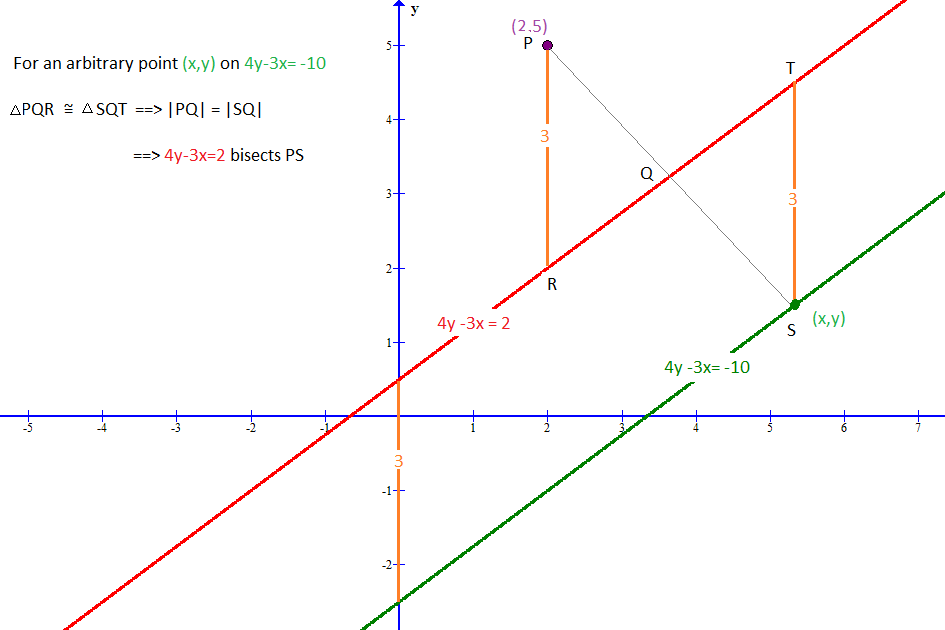
A line segment is bisected by a line with the equation # 4 y - 3 x = 2 #. If one end of the line segment is at #( 2 , 5 )#, where is the other end?
1 Answer
Oct 5, 2016
The other end will be any point on the line
Explanation:
Consider the vertical line
that is
Any point
Re-writing
The y-intercept for a line
Therefore this second line will have a slope-intercept equation of
or in a form similar to the initial equation:
The image below may help: