Question

A line segment is bisected by a line with the equation `4 y + 3 x = 2`. If one end of the line segment is at `( 2 , 1 )`, where is the other end?

Answer 1

One possible other end would be at `color(green)(""(2,-3))`
The equation of all possible answers is `color(green)(2x+4y=-6)`
If the given equation is to be the perpendicular bisector: `color(green)(""(2/25,-39/25))`

Explanation:

`K: 4y+3x=2` (the given bisecting line)

Let `H` be a vertical line through the given end point `(2,1)`.
Since `H` is a vertical line all values of `x in H` are equal to `2`
and `H` intersects `K` at `(2,-1)`

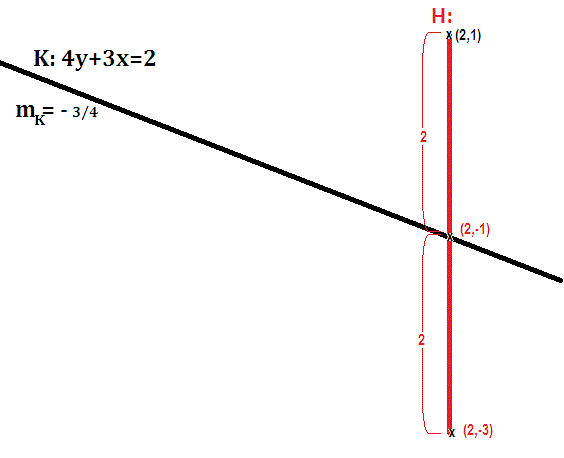
The distance from `(2,1)` to the intersection point `(2,-1)` is `2` units.
Moving another `2` units down `H` would bring us to `(2,-3)`

`K` bisects the line segment from `(2,1)` to `color(green)(""(2,-3))`
i.e. `color(green)(""(2,-3))` is one possible solution value to the given question.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

If we wanted the equation for all solution values
Consider a line `L` drawn through the point `(2,-3)` parallel to `K`

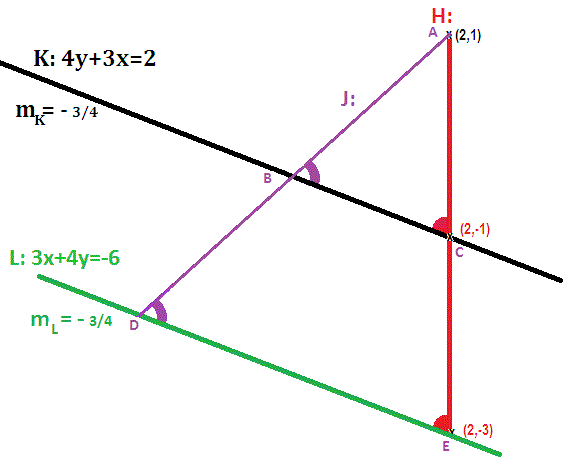
Note the labeling of Line Segment `H` into `AC` and `CD`
which we know from the previous work are in the ratio `1:1`

Consider any other arbitrary Line Segment `J` from `A` at `(2,1)` to the Line `L`.
Note again the labeling that divides `J` into segments `AB` and `BC`

Since `triangle ABC` and `triangle ADE` are similar,
the ratio of `abs(AB):abs(BD)=abs(AC):abs(CE)=1:1`

That is any arbitrary line segment connecting `(2,1)` and line `L` is bisected by `K`

Since `L` has the same slope as `K` and passes through `(2,-3)`
its equation is
`color(white)("XXX")y+3=(-3/4)(x-2)`
or
`color(white)("XXX")3x+4y=-6`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

If we wanted `K` to be a `underline(color(black)("perpendicular"))` bisector of the line segment

Consider the line `M` perpendicular to `K` through `(2,1)`

Since the slope of `K` is `m_K=-3/4`
the slope of `M` must be `m_M=4/3`

and the equation of `M` must be
`color(white)("XXX")(y+3)=4/3(x-2)`
or
`color(white)("XXX")4x-3y=5`

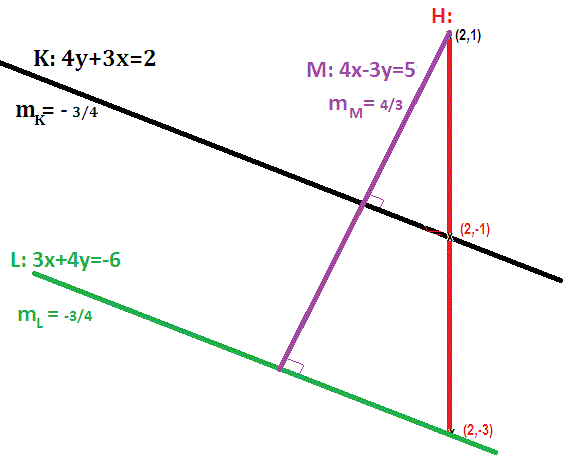
The endpoint of this perpendicular line segment can be derived as the intersection of `M` and `L`

`{(4x-3y=5),(3x+4y=-6):}`

Which gives `(x,y)=(2/25,-39/25)`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

My apologies for the length of this solution.

If anyone can provide a complete solution more briefly, please post it.