Question

A line segment is bisected by a line with the equation `4 y - 6 x = 8`. If one end of the line segment is at `( 7 , 3 )`, where is the other end?

Answer 1

Any point on the line `color(purple)(2y-3x=23)`
or
if the given line `color(red)(4y-6x=8)` is to be a perpendicular bisector then `color(brown)(""(-23/15,46/5))`

Explanation:

Apology:
Even omitting some details, this explanation is quite long.

Consider the vertical line `x=7` which passes through the given point `(7,3)`
This vertical line will intersect `color(red)(4y-6x=8)` at `(7,25/2)`, a point which is `25/2-3=19/2` above the given point `color(green)(""(7,3))`
A point twice as far above `color(green)(""(7,3))` would be at `(7,3+2xx19/2)=(7,22)`
That is the line segment from `color(green)(""(7,3))` to `(7,22)` is bisected by `color(red)("4y-6x=8)`

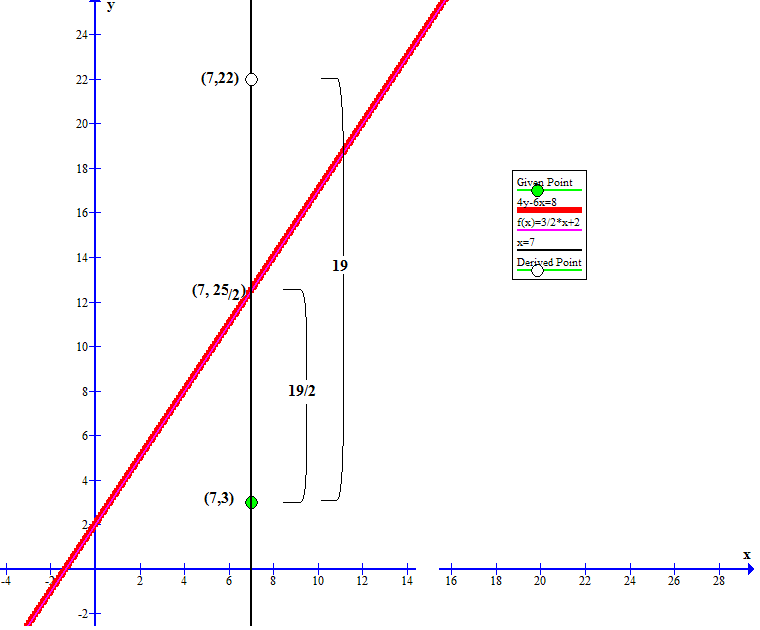
Furthermore, as we can see from similar triangles any line parallel to `color(red)(4y-6x=8)` and through `(7,22)` gives an infinite collection of points, any one of which would serve as an endpoint with `color(green)(""(7,3))` for a line segment bisected by `color(red)(4y-6x=8)`

`color(red)(4y-6x=8)` has a slope of `3/2`
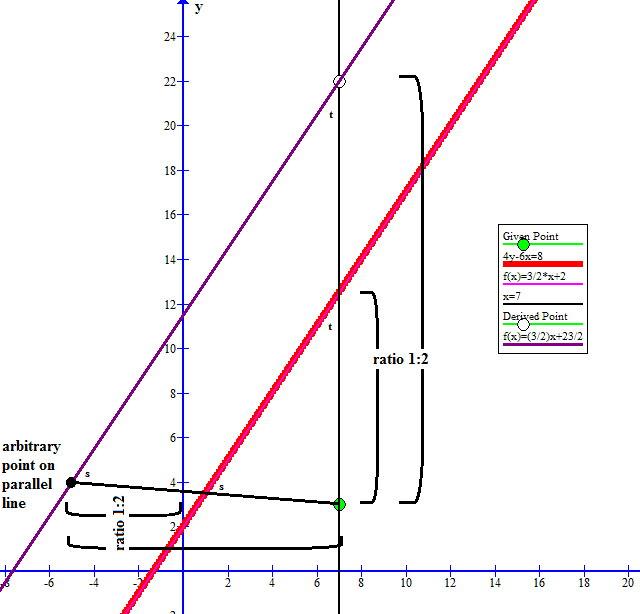
so any line parallel to it must also have a slope of `3/2`
and
if such a line passes through `(7,22)` then we can write its equation using the slope-point form:
`color(white)("XXX")y-22=3/2(x-7)`
or simplified as
`color(white)("XXX")color(purple)(2y-3x=23)`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

It is possible, since this question was asked under the heading "Perpendicular Bisectors" that it was intended that `color(red)(4y-6x=8)` should be the perpendicular bisector of a derived line segment.

In this case the perpendicular line to `color(red)(4y-6x=8)` passing through `color(green)(""(7,3))`
would have a slope of `-2/3` (the negative inverse of `color(red)(4y-6x=8)` and (again, working through the slope-point form)
an equation of `color(brown)(3y+2x=23)`

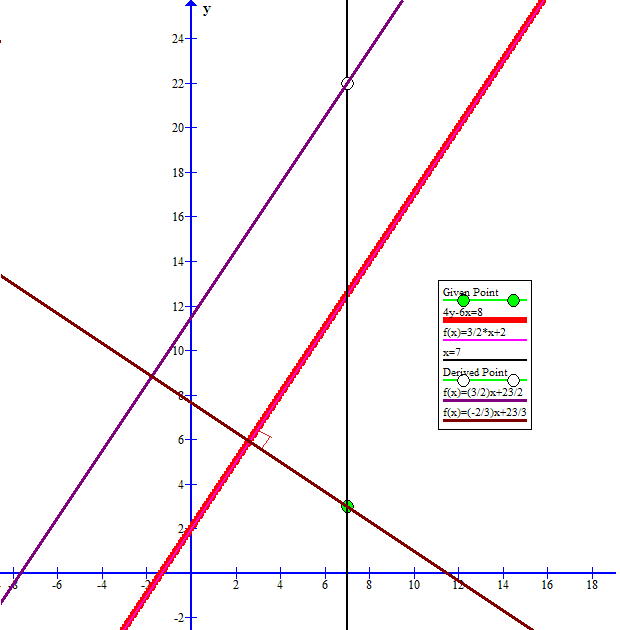
The system of equations:
`color(purple)(2y-3x=23)`
`color(brown)(3y+2x=23)`
can be solved for the point of intersection: `color(brown)(""(-23/15,46/5))`