Question

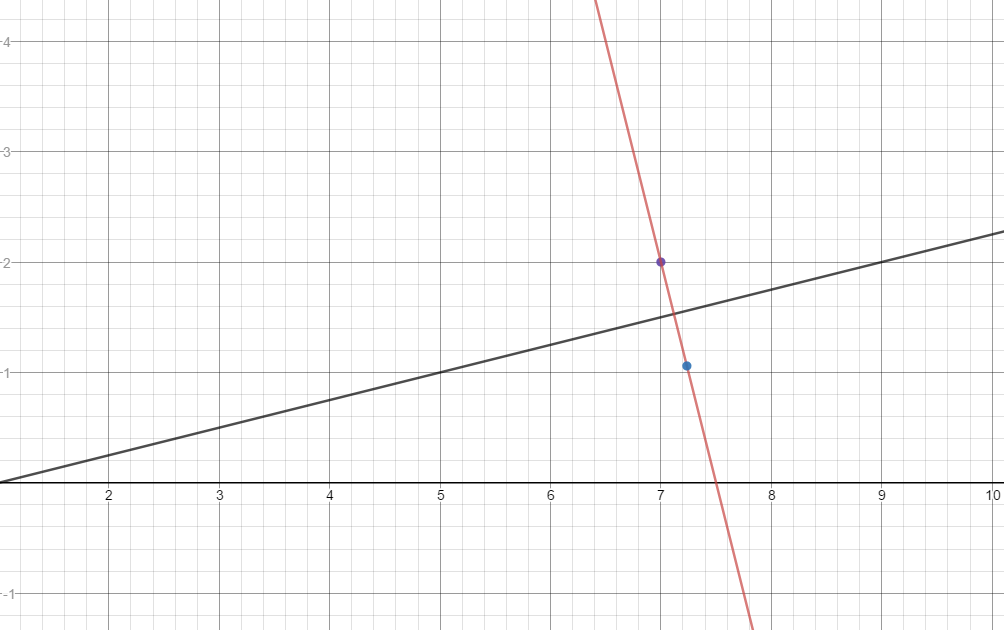
A line segment is bisected by a line with the equation `- 4 y + x = 1`. If one end of the line segment is at `( 7 , 2 )`, where is the other end?

Answer 1

The other end is at `(123/17, 18/17)`

Explanation:

Let's write the given line in the form `ax + by = c`

`x - 4y = 1" [1]"`

The general equation of lines perpendicular to this line is:

`4x + y = c`

To find the value of c, substitute 7 for x and 2 for y:

`4(7) + 2 = c`

`c = 30`

The equation of the bisected line segment is:

`4x + y = 30" [2]"`

The midpoint is at the intersection of of these two lines:

`x - 4y = 1" [1]"`
`4x + y = 30" [2]"`

Multiply equation [1] by 4 and subtract from equation [2]

`17y = 26`

`y = 26/17`

Let `Deltay =` the change in the y coordinate = `26/17 - 2`

The y coordinate of the other end of the line, `y_1` will have 2 twice the change from the starting y coordinate:

`y_1 = 2Deltay + y_0`

`y_1 = 2(26/17 - 2) + 2`

`y_1 = 52/17 - 2`

`y_1 = 18/17`

To find the corresponding x coordinate, substitute `18/17` for y into equation [2]:

`4x + 18/17 = 30`

`4x = 30 - 18/17`

`x_1 = 123/17`

The other end is at `(123/17, 18/17)`

Here is a graph of two lines and two points: