Question

A line segment is bisected by a line with the equation `- 5 y + 3 x = 1`. If one end of the line segment is at `(6 ,4 )`, where is the other end?

Answer 1

`-5y+3x=1` is the bisector for a line segment between `(6,4)` and any point on the line `color(blue)(-5y+3x=4)`

Explanation:

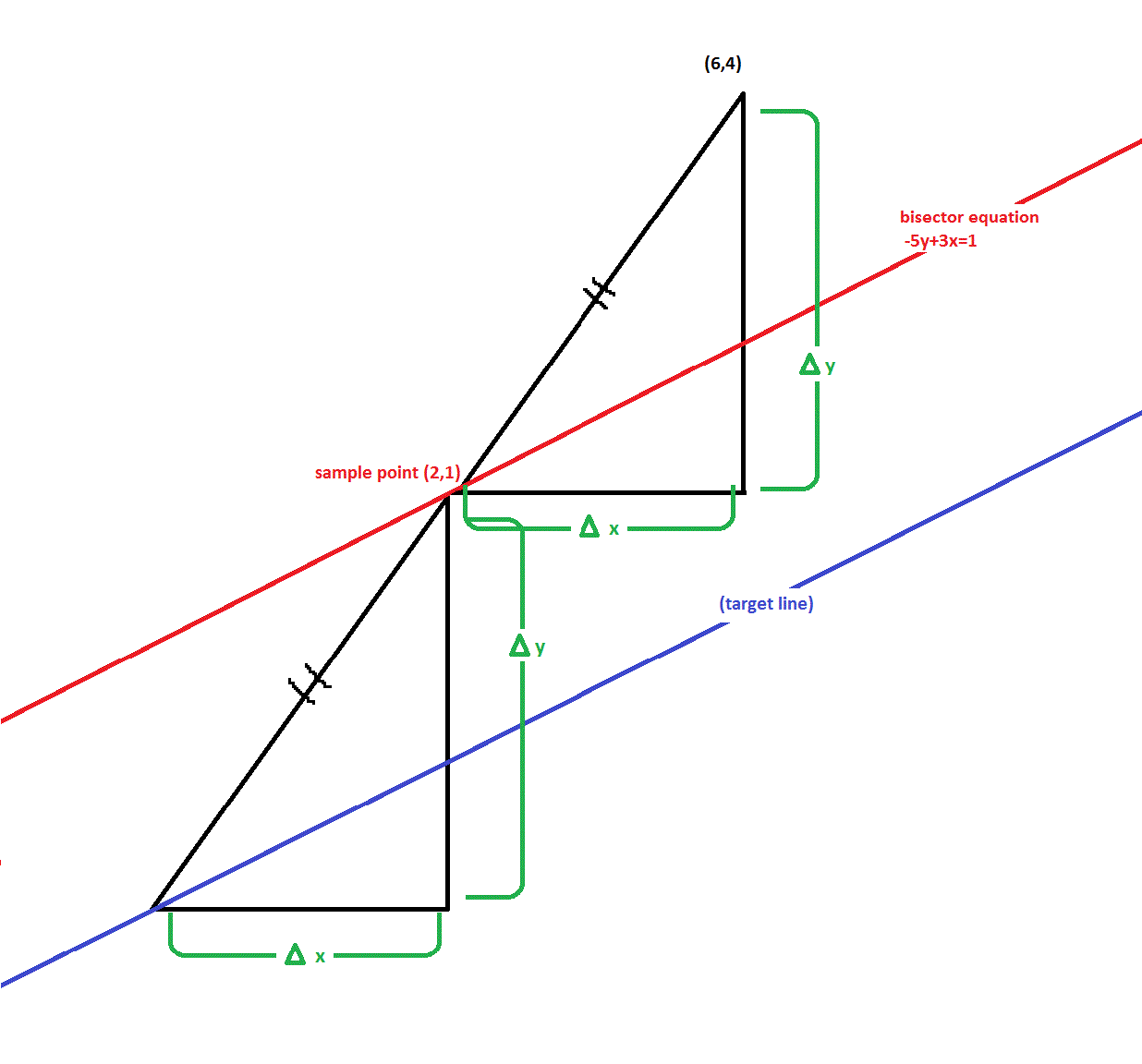
If `(x,y)` is the end point of a line segment with `(6,4)` as its other end; and
if `-5y+3x=1` bisects this line

Then for any point `(barx,bary)` on `-5y+3x=1`
the `Deltax` and `Deltay` between `(6,4)` and `(barx,bary)`
will be the same as `Deltax` and `Deltay` between `(barx,bary)` and the corresponding target end point.

Since `Deltax=6-barx` and `Deltay=4-bary`
for any point `(barx,bary)` on `-5y+3x=1`
the corresponding target end point will be `(2barx-6,2bary-4)`

Specifically we can see that `(barx,bary)=(2,1)` is a point on `-5y+3x=1`
with a corresponding target point of `(-2,-2)`

Note also that the target line is parallel to `-5y+3x=1`
and therefore has the same slope (namely `3/5`).

Using the slope-point form for the target line, we get
`color(white)("XXX")(y+2)=3/5(x+2)`
or
`color(white)("XXX")5y+10=3x+6`
or
`color(white)("XXX")-5y+3x=4`