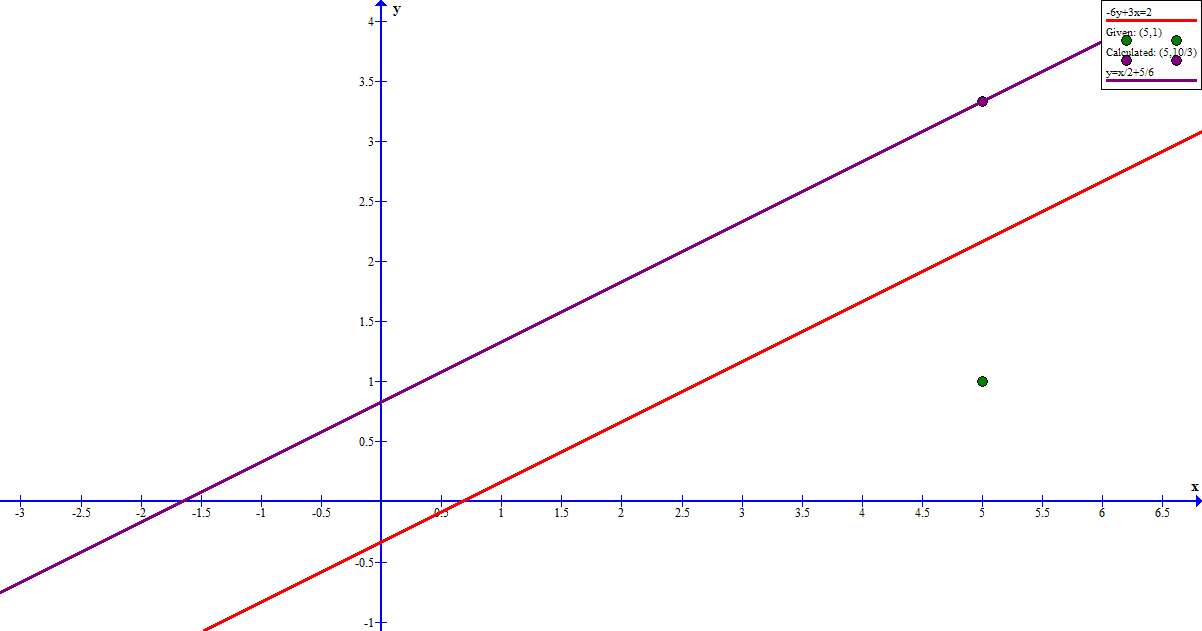
#color(red)(-6y+3x=2)# can be rewritten as #color(red)(y=1/2x-1/3)#
When #x=5#
#color(white)("XXX")y=1/2x-1/3color(white)("XX")rarrcolor(white)("XX")y=color(red)(13/6)#
The vertical distance from #color(green)(""(5,1))# to the point #color(red)(""(5,13/6))# on the line #color(red)(-6y+3x=2)# is
#color(white)("XXX")color(blue)(13/6-1=7/6)#
That is moving vertically the line #color(red)(-6y+3x=2)# is #color(blue)(7/6)# above the point #color(green)(""(5,1))#.
If we continue moving upward another #color(blue)(7/6)# units (for a total of #14/6=7/3# units above #color(green)(""(5,1))#)
we will reach the point #""(5,10/3))#
which will be the same distance above #color(red)(-6y+3x=2)# as #color(green)(""(5,1))# is below it.
That is #color(red)(-6y+3x=2)# bisects the line segment joining #color(green)(""(5,1))# and #color(purple)(""(5,10/3))#
In fact the line segment between #color(green)(""(5,1))# and any point on the line parallel to #color(red)(-6y+3x=2)# through #color(purple)(""(5,10/3))# will be bisected by #color(red)(-6y+3x=2)#
#color(red)(-6y+3x=2)# has a slope of #color(red)(1/2)#
so the line through #color(purple)(""(5,10/3))# will also have a slope of #color(red)(1/2)#
and using the slope-point form, it will have an equation of
#color(white)("XXX")y-color(purple)(10/3)=color(red)(1/2)(x-color(purple)(5))#
which can be simplified as
#color(white)("XXX")y=x/2+5/6#